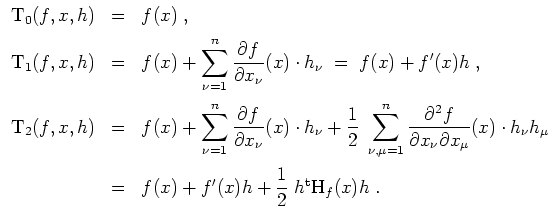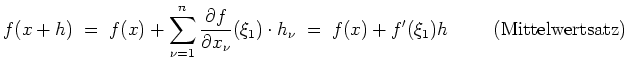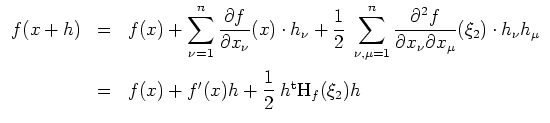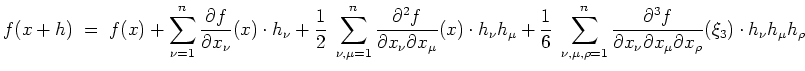Mittelwertsatz.
Es seien
![]() ,
,
![]() eine offene Menge und
eine offene Menge und
![]() differenzierbar.
differenzierbar.
Es seien ferner
![]() derart, daß die Verbindungsstrecke
derart, daß die Verbindungsstrecke
Dann besagt der Mittelwertsatz, daß es ein
![]() gibt mit
gibt mit
Gebiete.
Es seien
![]() ,
,
![]() eine Menge, und
eine Menge, und
![]() .
.
Unter einer Kurve in
![]() von
von
![]() nach
nach
![]() versteht man eine stetige Abbildung
versteht man eine stetige Abbildung
![]() mit
mit
![]() und
und
![]() .
.
Ist z.B.
![]() , so ist
, so ist
![]() eine Kurve in
eine Kurve in
![]() von
von
![]() nach
nach
![]() .
.
Eine Menge
![]() derart, daß für alle
derart, daß für alle
![]() eine Kurve in
eine Kurve in
![]() von
von
![]() nach
nach
![]() existiert,
heißt zusammenhängend. Ein Gebiet ist eine offene, zusammenhängende Menge.
existiert,
heißt zusammenhängend. Ein Gebiet ist eine offene, zusammenhängende Menge.
Eine Menge
![]() derart, daß für alle
derart, daß für alle
![]() die Verbindungsstrecke
die Verbindungsstrecke
![]() in
in
![]() liegt, heißt konvex.
Ist
liegt, heißt konvex.
Ist
![]() konvex, so ist
konvex, so ist
![]() auch zusammenhängend.
auch zusammenhängend.
Es seien
![]() ein Gebiet und
ein Gebiet und
![]() differenzierbar mit
differenzierbar mit
![]() für
alle
für
alle
![]() . Dann ist
. Dann ist
![]() konstant, i.e. es ist
konstant, i.e. es ist
![]() für alle
für alle
![]() .
.
Satz von Taylor.
Sei
![]() offen. Sei
offen. Sei
![]() eine
eine
![]() -fach stetig differenzierbare Funktion.
-fach stetig differenzierbare Funktion.
Unter einem Multiindex verstehen wir ein Tupel
![]() .
.
Wir setzen
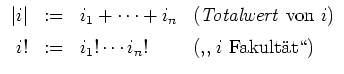
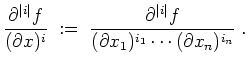
Das
![]() -te Taylorpolynom von
-te Taylorpolynom von
![]() an der Stelle
an der Stelle
![]() in der Variablen
in der Variablen
![]() ist definiert durch
ist definiert durch
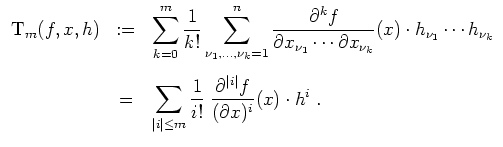
Beachte, daß in der ersteren Summendarstellung die Indizes
![]() nicht notwendig paarweise verschieden sind. Ferner tauchen dank des
Satzes von Schwarz darin Terme mehrfach auf. In der zweiten Summendarstellung sind diese mehrfachen Terme zusammengefaßt.
nicht notwendig paarweise verschieden sind. Ferner tauchen dank des
Satzes von Schwarz darin Terme mehrfach auf. In der zweiten Summendarstellung sind diese mehrfachen Terme zusammengefaßt.
Sei nun
![]() derart, daß
derart, daß
![]() .
Dann besagt der Satz von Taylor, daß es solch ein
.
Dann besagt der Satz von Taylor, daß es solch ein
![]() gibt, daß
gibt, daß
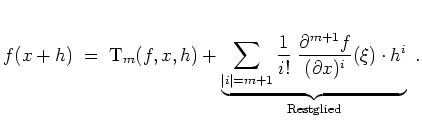
Der Mittelwertsatz ist der Spezialfall
![]() des Satzes von Taylor.
des Satzes von Taylor.
Wir erhalten z.B. die Taylorpolynome