Sei
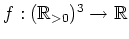 definiert durch
definiert durch
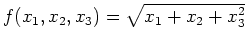 . Sei
. Sei
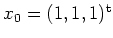 . Sei
. Sei
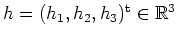 variabel.
variabel.
- 1.
- Berechne das 2. Taylorpolynom
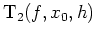 .
.
- 2.
- Sei
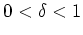 . Schätze
. Schätze
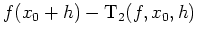 für
für
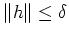 mittels Satz von Taylor dergestalt ab, daß die
gefundene obere Schranke nicht von
mittels Satz von Taylor dergestalt ab, daß die
gefundene obere Schranke nicht von
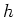 abhängt. Optimalität dieser Schranke ist nicht verlangt, wohl aber sollte sie von Ordnung
abhängt. Optimalität dieser Schranke ist nicht verlangt, wohl aber sollte sie von Ordnung
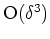 sein für
sein für
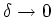 .
.
![]() definiert durch
definiert durch
![]() . Sei
. Sei
![]() . Sei
. Sei
![]() variabel.
variabel.