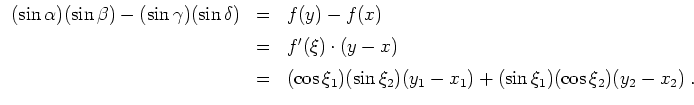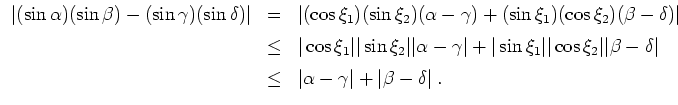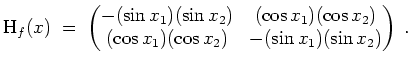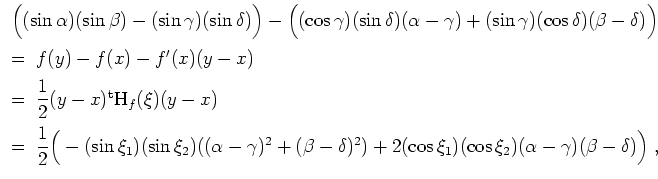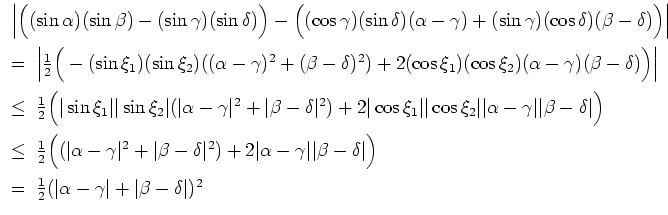Es sei
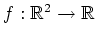 definiert durch
definiert durch
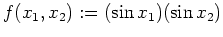 . Dann ist
. Dann ist
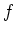 beliebig oft differenzierbar.
beliebig oft differenzierbar.
- 1.
- Es ist
Wir setzten
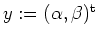 und
und
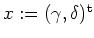 . Dann gibt es nach dem Mittelwertsatz so
ein
. Dann gibt es nach dem Mittelwertsatz so
ein
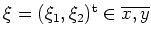 , daß
Also folgt
, daß
Also folgt
- 2.
- Es ist
Wir setzten
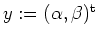 und
und
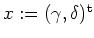 . Nach dem Satz von Taylor gibt es so ein
. Nach dem Satz von Taylor gibt es so ein
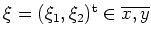 , daß
woraus
folgt.
, daß
woraus
folgt.
![]() definiert durch
definiert durch
![]() . Dann ist
. Dann ist
![]() beliebig oft differenzierbar.
beliebig oft differenzierbar.