Es sei
![]() gegeben. Wir müssen so ein
gegeben. Wir müssen so ein
![]() finden, daß
finden, daß
Es gilt für alle
![]()
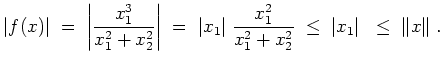
Im Punkt
![]() gilt
gilt
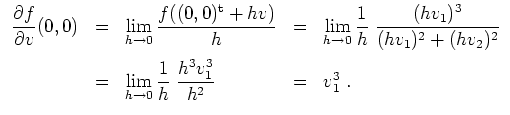
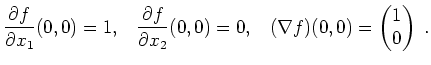
Alternativ kann man die Definition der partiellen Ableitung verwenden.
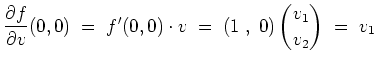
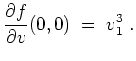
Es sei
![]() gegeben. Wir müssen so ein
gegeben. Wir müssen so ein
![]() finden, daß
finden, daß
Es gilt für alle
![]()
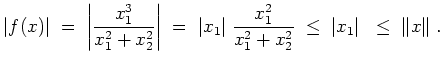
Im Punkt
![]() gilt
gilt
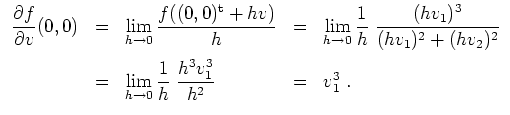
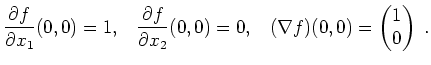
Alternativ kann man die Definition der partiellen Ableitung verwenden.
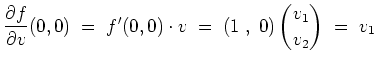
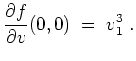
Skizze von
![]() .
.
![\includegraphics[width = 8cm]{s2.eps}](img27.png)