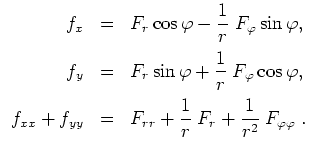- (a)
-
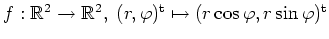 (Polarkoordinaten).
(Polarkoordinaten).
- (b)
-
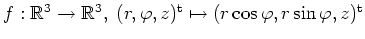 (Zylinderkoordinaten).
(Zylinderkoordinaten).
- (c)
-
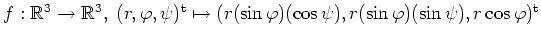 (Kugelkoordinaten).
(Kugelkoordinaten).
Berechne alle partiellen Ableitungen erster und zweiter Ordnung von
![]() . Zeige, daß im Punkt
. Zeige, daß im Punkt
![]() folgendes gilt.
folgendes gilt.
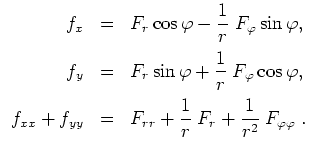
Berechne alle partiellen Ableitungen erster und zweiter Ordnung von
![]() . Zeige, daß im Punkt
. Zeige, daß im Punkt
![]() folgendes gilt.
folgendes gilt.