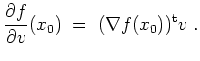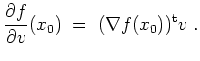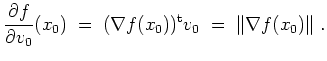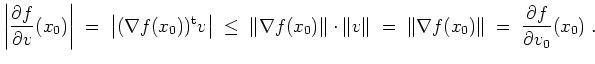Lösung.

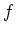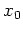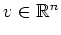Da $ \mbox{$f$}$ differenzierbar ist im Punkt $ \mbox{$x_0$}$ , ist für alle Richtungen $ \mbox{$v\in\mathbb{R}^n$}$
$ \mbox{$\displaystyle \frac{\partial f}{\partial v}(x_0) \;=\; (\nabla f(x_0))^\text{t} v\;. $}$
Speziell wird
$ \mbox{$\displaystyle \frac{\partial f}{\partial v_0}(x_0) \;=\; (\nabla f(x_0))^\text{t} v_0 \;=\; \Vert\nabla f(x_0)\Vert\;. $}$

Mit der Cauchy-Schwarzschen Ungleichung folgt

$ \mbox{$\displaystyle \left\vert\frac{\partial f}{\partial v}(x_0)\right\vert ... ... \;=\; \Vert\nabla f(x_0)\Vert \;=\; \frac{\partial f}{\partial v_0}(x_0)\;. $}$
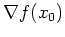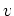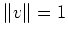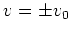In der Cauchy-Schwarzschen Ungleichung tritt die Gleichheit genau dann ein, wenn $ \mbox{$\nabla f(x_0)$}$ und $ \mbox{$v$}$ linear abhängig sind. Wegen $ \mbox{$\Vert v\Vert=1$}$ ist dies gleichbedeutend mit $ \mbox{$v=\pm v_0$}$ .