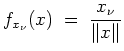
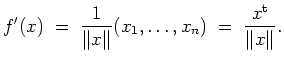
Eine alternative Berechnung ergibt sich aus den Ableitungsregeln zu
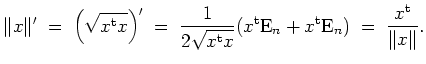
Die Hessematrix läßt sich mit den Methoden der eindimensionalen Analysis bestimmen zu
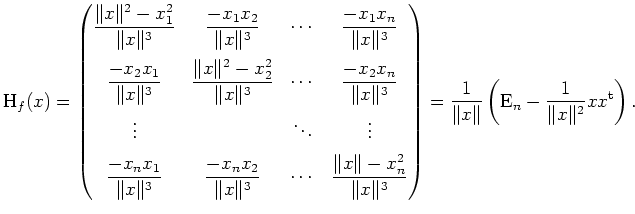
Alternativ kann man mit der Produkt- und Kettenregel wie folgt argumentieren.
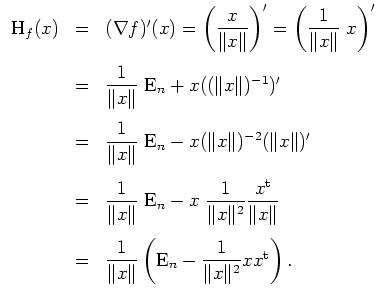
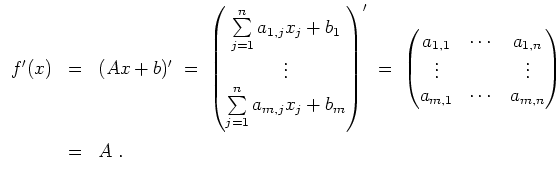
Die Hessematrix ist nur für Funktionen erklärt, die in die reellen Zahlen
![]() abbilden. Folglich existiert
die Hessematrix von
abbilden. Folglich existiert
die Hessematrix von
![]() nur im Fall
nur im Fall
![]() .
.
In diesem Fall sind die ersten partiellen Ableitungen konstant und folglich ergibt sich die Hessematrix von
![]() zu
zu
![]() .
.