Die gegebene Funktion
![]() ist als Komposition differenzierbarer Funktionen
differenzierbar in allen Punkten
ist als Komposition differenzierbarer Funktionen
differenzierbar in allen Punkten
![]() mit
mit
![]() . Damit existieren insbesondere auch alle
Richtungsableitungen von
. Damit existieren insbesondere auch alle
Richtungsableitungen von
![]() in diesen Punkten.
in diesen Punkten.
Wir untersuchen nun die Existenz der Richtungsableitung von
![]() in dem Punkt
in dem Punkt
![]() in Richtung
in Richtung
![]() .
Dabei unterscheiden wir zwei Fälle.
.
Dabei unterscheiden wir zwei Fälle.
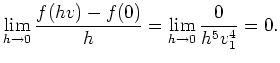
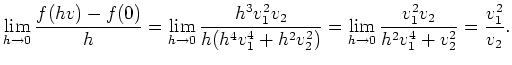
Wir zeigen nun, daß die Funktion
![]() nicht differenzierbar ist, indem wir zeigen, daß sie nicht
stetig im Punkt
nicht differenzierbar ist, indem wir zeigen, daß sie nicht
stetig im Punkt
![]() ist.
ist.
Für die Folge
![]() mit
mit
![]() ist nämlich
ist nämlich
![]() für
für
![]() , wohingegen
, wohingegen
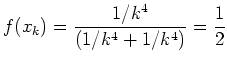
Skizze von
![]() .
.
![\includegraphics[width = 8cm]{l2.eps}](img21.png)