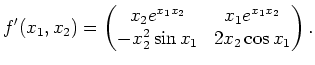Um die partielle Ableitung nach
![]() zu berechnen, sehen wir die übrigen Variablen, d.h.
zu berechnen, sehen wir die übrigen Variablen, d.h.
![]() , als konstant an und erhalten mit
den Regeln der eindimensionalen Analysis
, als konstant an und erhalten mit
den Regeln der eindimensionalen Analysis
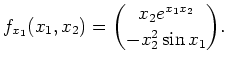
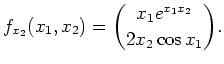
Da die beiden partiellen Ableitungen von
![]() stetig als Komposition stetiger Funktionen sind, ist
stetig als Komposition stetiger Funktionen sind, ist
![]() insbesondere
(total) differenzierbar und es gilt
insbesondere
(total) differenzierbar und es gilt