- 1.
- Bestimme jeweils die partiellen Ableitungen von
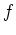 und stelle fest, daß diese stetig sind.
und stelle fest, daß diese stetig sind.
Verwende darüberhinaus die Identität
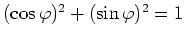 für
für
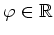 .
.
- 2.
- Benutze die Kettenregel, um die Funktion
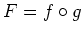 zu differenzieren, wobei
zu differenzieren, wobei
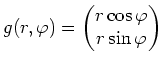 .
Bestimme damit die partiellen Ableitungen von
.
Bestimme damit die partiellen Ableitungen von
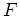 . Löse die Gleichungen nach
. Löse die Gleichungen nach
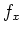 und
und
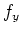 auf.
Verwende dieses Ergebnis nun für
auf.
Verwende dieses Ergebnis nun für
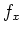 bzw.
bzw.
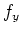 anstelle von
anstelle von
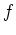 und berechne so
und berechne so
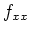 und
und
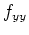 .
.
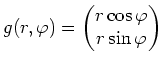 .
Bestimme damit die partiellen Ableitungen von
.
Bestimme damit die partiellen Ableitungen von
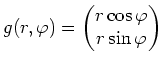 .
Bestimme damit die partiellen Ableitungen von
.
Bestimme damit die partiellen Ableitungen von