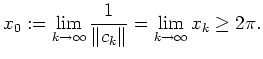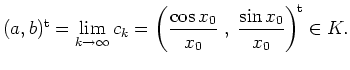Da
![]() stetig ist, folgt
stetig ist, folgt
![]() für
für
![]() .
Ferner gilt
.
Ferner gilt
![]() für alle
für alle
![]() . Für
. Für
![]() folgt daher
folgt daher
![]() , d.h.
, d.h.
![]() .
.
Damit haben wir gezeigt, daß die Menge
![]() alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.
alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.
Betrachte nun die Funktion
![]() . Dann gilt
. Dann gilt
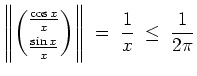
Sei nun
![]() ein Berührpunkt von
ein Berührpunkt von
![]() . Wir wollen zeigen, daß
. Wir wollen zeigen, daß
![]() ist.
ist.
Sei dazu
![]() eine konvergente Folge mit
eine konvergente Folge mit
![]() und
und
![]() .
Wir können ohne Einschränkung annehmen, daß
.
Wir können ohne Einschränkung annehmen, daß
![]() und
und
![]() für alle
für alle
![]() .
Es ist also
.
Es ist also
![]() für gewisse
für gewisse
![]() .
.
Da die Folge
![]() in
in
![]() konvergiert, existiert der Grenzwert
konvergiert, existiert der Grenzwert