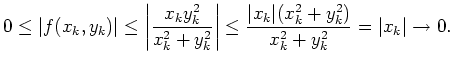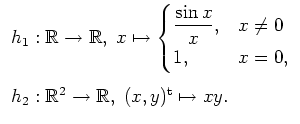- 1.
- Es seien
Es ist
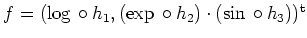 . Damit ist jede Komponente von
. Damit ist jede Komponente von
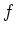 als Produkt von Kompositionen stetiger Funktionen stetig. Die Funktion
als Produkt von Kompositionen stetiger Funktionen stetig. Die Funktion
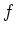 ist demzufolge stetig.
ist demzufolge stetig.
- 2.
- Die Funktion
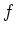 ist nicht stetig. Betrachte nämlich z.B. die Folge
ist nicht stetig. Betrachte nämlich z.B. die Folge
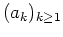 , definiert durch
Es konvergiert
, definiert durch
Es konvergiert
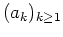 gegen
gegen
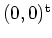 . Andererseits ist
. Andererseits ist
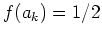 für alle
für alle
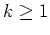 und damit
ist auch
und damit
ist auch
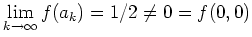 . Daher ist die Funktion
. Daher ist die Funktion
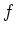 nicht stetig.
nicht stetig.
Alternativ kann man die Abbildung
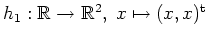 betrachten. Wäre
betrachten. Wäre
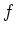 stetig, so wäre auch
die Abbildung
stetig, so wäre auch
die Abbildung
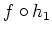 stetig. Es gilt jedoch
stetig. Es gilt jedoch
Da diese Funktion unstetig ist, kann auch
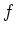 nicht stetig gewesen sein.
nicht stetig gewesen sein.
- 3.
- Die Funktion
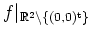 ist stetig, da sie auf diesem Definitionsbereich
Quotient von
Polynomen ist. Um die Funktion
ist stetig, da sie auf diesem Definitionsbereich
Quotient von
Polynomen ist. Um die Funktion
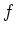 auf Stetigkeit zu untersuchen, genügt es also, den Ursprung zu betrachten.
auf Stetigkeit zu untersuchen, genügt es also, den Ursprung zu betrachten.
Es sei
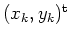 eine Folge, die gegen den Punkt
eine Folge, die gegen den Punkt
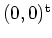 konvergiert. Dann gilt
konvergiert. Dann gilt
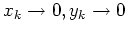 für
für
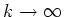 , und daher
, und daher
Also gilt
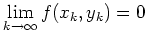 für alle Folgen
für alle Folgen
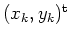 , die gegen
, die gegen
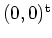 konvergieren. Daher ist
konvergieren. Daher ist
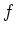 stetig im Punkt
stetig im Punkt
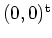 und folglich insgesamt stetig.
und folglich insgesamt stetig.
- 4.
- Es seien
Die Funktion
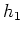 ist stetig, wie aus der eindimensionalen Analysis bekannt ist (es sei etwa an die
Potenzreihenentwicklung der Sinusfunktion erinnert). Die Funktion
ist stetig, wie aus der eindimensionalen Analysis bekannt ist (es sei etwa an die
Potenzreihenentwicklung der Sinusfunktion erinnert). Die Funktion
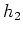 ist stetig als Polynom. Daher ist auch
ist stetig als Polynom. Daher ist auch
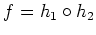 stetig.
stetig.
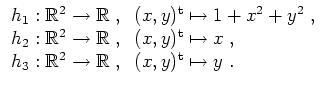
![]() . Damit ist jede Komponente von
. Damit ist jede Komponente von
![]() als Produkt von Kompositionen stetiger Funktionen stetig. Die Funktion
als Produkt von Kompositionen stetiger Funktionen stetig. Die Funktion
![]() ist demzufolge stetig.
ist demzufolge stetig.
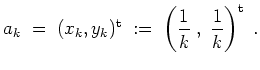
![]() betrachten. Wäre
betrachten. Wäre
![]() stetig, so wäre auch
die Abbildung
stetig, so wäre auch
die Abbildung
![]() stetig. Es gilt jedoch
stetig. Es gilt jedoch
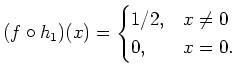
![]() eine Folge, die gegen den Punkt
eine Folge, die gegen den Punkt
![]() konvergiert. Dann gilt
konvergiert. Dann gilt
![]() für
für
![]() , und daher
, und daher