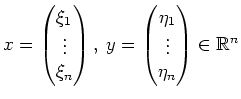 .
.
Norm, Folgenkonvergenz und Abschluß.
Seien
![]() .
Seien
.
Seien
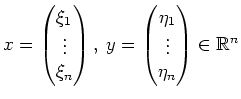 .
.
Wir erinnern an das Skalarprodukt
![]() und die (euklidische) Norm
und die (euklidische) Norm
![]() .
.
Die (euklidische) Norm erfüllt folgende drei Eigenschaften für alle
![]() :
:
Eine Folge
![]() konvergiert gegen einen Punkt
konvergiert gegen einen Punkt
![]() , wenn für alle
, wenn für alle
![]() ein
ein
![]() so
existiert, daß
so
existiert, daß
Schreibweise:
![]() oder
oder
![]() .
.
Der Grenzwert einer Folge ist eindeutig bestimmt, falls er existiert.
Es sei
![]() . Ein Punkt
. Ein Punkt
![]() heißt Berührpunkt von
heißt Berührpunkt von
![]() , falls
für jedes
, falls
für jedes
![]() die (offene)
die (offene)
![]() -Umgebung
-Umgebung
Funktionsgrenzwerte.
Sei
![]() eine Teilmenge, und sei
eine Teilmenge, und sei
![]() eine Funktion.
eine Funktion.
Es heißt
![]() der Grenzwert von
der Grenzwert von
![]() an der Stelle
an der Stelle
![]() , falls es für alle
, falls es für alle
![]() ein
ein
![]() gibt mit
gibt mit
Nach dem Folgenkriterium konvergiert
![]() gegen
gegen
![]() an der Stelle
an der Stelle
![]() , falls für alle Folgen
, falls für alle Folgen
![]() mit
mit
![]() und
und
![]() gilt, daß
gilt, daß
![]() .
.
Stetigkeit.
Sei
![]() eine Teilmenge, und sei
eine Teilmenge, und sei
![]() eine Funktion.
eine Funktion.
Die Funktion
![]() heißt stetig im Punkt
heißt stetig im Punkt
![]() , wenn
, wenn
Die Funktion
![]() heißt stetig, wenn sie in allen Punkten
heißt stetig, wenn sie in allen Punkten
![]() stetig ist.
stetig ist.
Ist
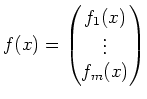 mit Koordinatenfunktionen
mit Koordinatenfunktionen
![]() , so ist
, so ist
![]() stetig in
stetig in
![]() genau dann, wenn
genau dann, wenn
![]() stetig in
stetig in
![]() sind.
sind.
Ist
![]() ein Polynom, d.h. gilt
ein Polynom, d.h. gilt
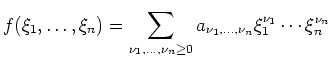
Für stetige Funktionen
![]() ,
,
![]() , wobei
, wobei
![]() , sowie
, sowie
![]() , sind auch die Funktionen
, sind auch die Funktionen
Satz von Weierstraß.
Eine Teilmenge
![]() heißt abgeschlossen, falls
heißt abgeschlossen, falls
![]() , d.h. falls
, d.h. falls
![]() alle seine
Berührpunkte enthält.
alle seine
Berührpunkte enthält.
Die Menge
![]() heißt beschränkt, falls
heißt beschränkt, falls
![]() , d.h. falls es ein
, d.h. falls es ein
![]() gibt, so daß
gibt, so daß
![]() für alle
für alle
![]() .
.
Die Menge
![]() heißt kompakt, falls sie abgeschlossen und beschränkt ist.
heißt kompakt, falls sie abgeschlossen und beschränkt ist.
Sei
![]() eine stetige Funktion auf einer nicht-leeren kompakten Menge
eine stetige Funktion auf einer nicht-leeren kompakten Menge
![]() .
Dann existieren nach dem Satz von Weierstraß
.
Dann existieren nach dem Satz von Weierstraß
![]() und
und
![]() , d.h. es gibt
, d.h. es gibt
![]() , so daß
, so daß
Satz von Heine-Borel.
Es sei
![]() eine Teilmenge. Unter einer offenen Überdeckung von
eine Teilmenge. Unter einer offenen Überdeckung von
![]() versteht man eine Familie
versteht man eine Familie
![]() von offenen Mengen
von offenen Mengen
![]() derart, daß
derart, daß
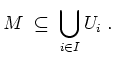
Der Satz von Heine-Borel besagt nun, daß die Menge
![]() genau dann kompakt ist, wenn jede offene Überdeckung von
genau dann kompakt ist, wenn jede offene Überdeckung von
![]() eine
endliche Teilüberdeckung besitzt.
eine
endliche Teilüberdeckung besitzt.