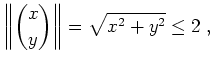
Sei ferner
![]() eine konvergente Folge mit
eine konvergente Folge mit
![]() für alle
für alle
![]() und
und
![]() . Dann gilt
. Dann gilt
![]() und
und
![]() für
für
![]() , und
, und
Dies bedeutet, daß die Menge
![]() alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.
alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.
Da
![]() beschränkt und abgeschlossen ist, ist sie kompakt.
beschränkt und abgeschlossen ist, ist sie kompakt.
Die Folge
![]() , definiert durch
, definiert durch
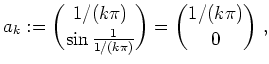
Da die Menge
![]() nicht abgeschlossen ist, kann sie insbesondere nicht kompakt sein.
nicht abgeschlossen ist, kann sie insbesondere nicht kompakt sein.
Es ist
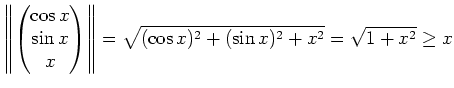
Nach dem Satz von Heine-Borel ist die Menge
![]() demnach kompakt.
demnach kompakt.