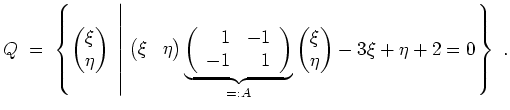
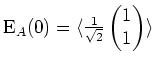 und
und
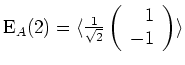 . Damit erhalten wir die unitäre Matrix
. Damit erhalten wir die unitäre Matrix
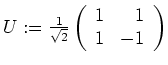 mit welcher sich die Diagonalisierung
mit welcher sich die Diagonalisierung
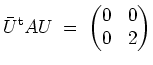
Wir halten zunächst fest, daß die Hauptachsen der Quadrik
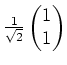 und
und
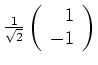 sind.
sind.
Wir substituieren
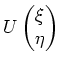 für
für
![]() , d.h.
, d.h.
![]() für
für
![]() und
und
![]() für
für
![]() , und erhalten die Gleichung
, und erhalten die Gleichung
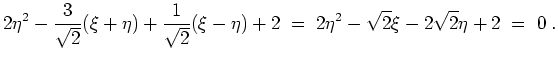
Nun setzen wir
![]() und substituieren
und substituieren
![]() für
für
![]() , um
, um
Schließlich setzen wir
![]() und substituieren
und substituieren
![]() für
für
![]() , um
, um
Nach Vertauschung von
![]() und
und
![]() und Division durch
und Division durch
![]() ist die Gleichung von der Form
ist die Gleichung von der Form
Der Scheitelpunkt der Parabel befindet sich also in
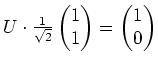 .
.
![\includegraphics[width = 10cm,height = 10cm]{parabel.eps}](img26.png)
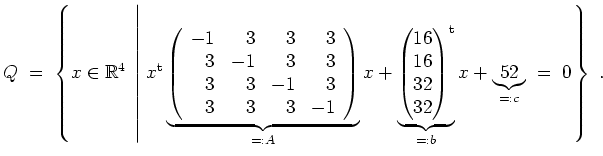
Um
![]() unitär zu diagonalisieren, bestimmen wir
unitär zu diagonalisieren, bestimmen wir
![]() sowie
sowie
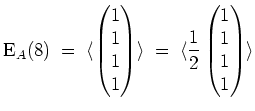
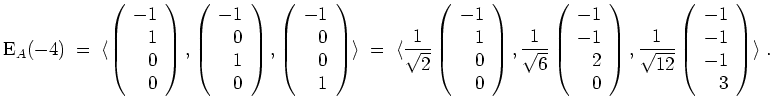
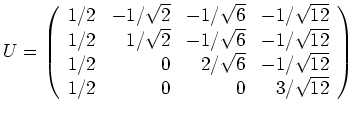
Wir halten fest, daß
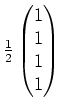 ,
,
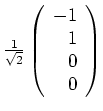 ,
,
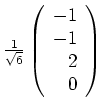 und
und
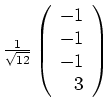 die Hauptachsen der Quadrik
die Hauptachsen der Quadrik
![]() sind.
sind.
Wir substituieren
![]() für
für
![]() und erhalten die Gleichung
und erhalten die Gleichung
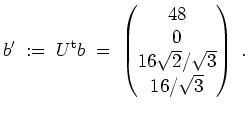
Nun setzen wir
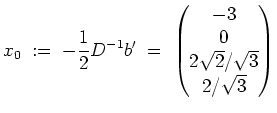
Es handelt sich bei
![]() also um ein
also um ein
![]() -Ellipso-
-Ellipso-
![]() -hyperboloid mit Mittelpunkt
-hyperboloid mit Mittelpunkt
![]() und Halbachse
und Halbachse
![]() .
.