Lösung.

1.
Da die Einträge auf der Hauptdiagonalen nicht sämtlich $ \mbox{$\leq 0$}$ sind, ist $ \mbox{$A$}$ nicht negativ semidefinit. Positive Semidefinitheit kann man nicht ausschließen, aber an dieser Stelle auch noch nicht bestätigen.

2.
Die Hauptminoren ergeben sich zu $ \mbox{$\det A_1=9$}$ , $ \mbox{$\det A_2=81$}$ , $ \mbox{$\det A_3=\det A_4 = \det A_5 =0$}$ . Daraus folgt, daß $ \mbox{$A$}$ nicht positiv definit und nicht negativ definit ist.

3.
Es wird
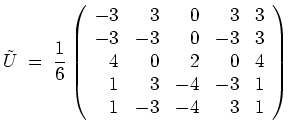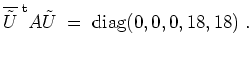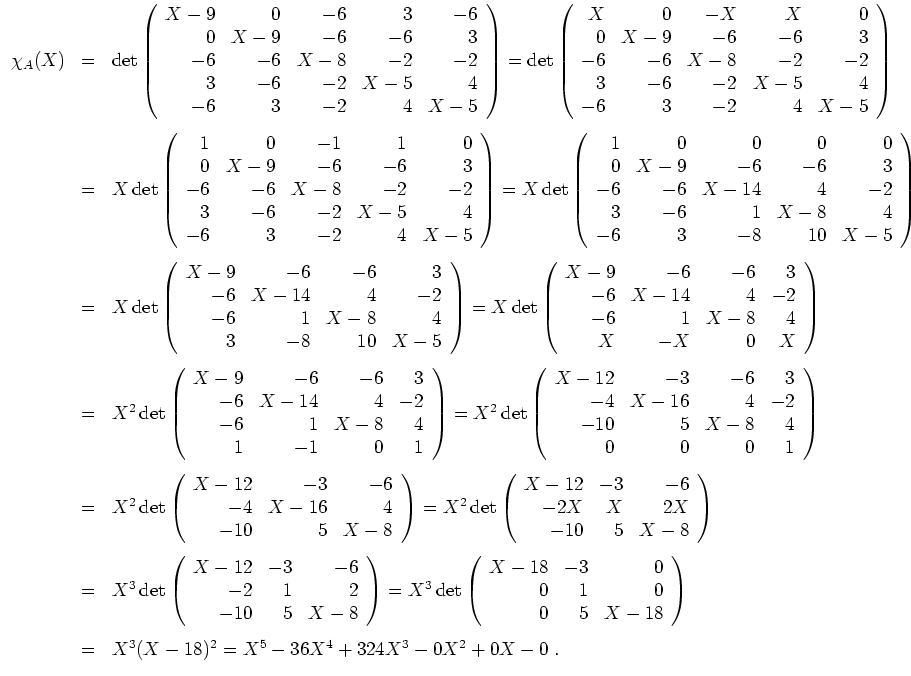
$ \mbox{$\displaystyle \begin{array}{rclcl} \chi_A(X) \par &=& \det\left(\begi... ...mm}\\ \par &=& X^3(X-18)^2 \par = X^5-36X^4+324X^3-0X^2+0X-0\;. \end{array}$}$

Damit ist $ \mbox{$A$}$ positiv semidefinit, weil die Koeffizienten abwechselndes Vorzeichen haben oder $ \mbox{$0$}$ sind.

Tatsächlich haben wir hier die Eigenwerte $ \mbox{$0$}$ und $ \mbox{$18$}$ von $ \mbox{$A$}$ berechnet, was ebenfalls positive Semidefinitheit nach sich zieht. Sogar die Signatur $ \mbox{$(2,0)$}$ kann abgelesen werden. Dies wäre allerdings schwierig, wenn $ \mbox{$\chi_A(X)$}$ nicht in faktorisierter Form hätte gefunden werden können.

4.
Mittels beidseitigem Gaußschen Algorithmus ergibt sich

$ \mbox{$\displaystyle \left(\begin{array}{rrrrr} 9& 0& 6& -3& 6\\ 0& 9& 6&... ... 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0 \end{array}\right)\;. $}$
Also ist die Signatur von $ \mbox{$A$}$ gleich $ \mbox{$(2,0)$}$ .

5.
Es ergibt sich
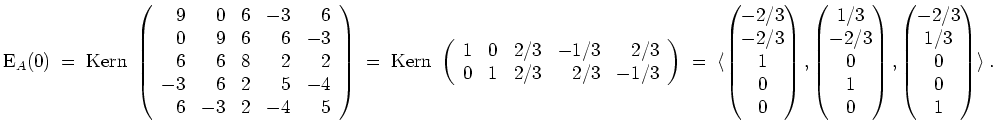
$ \mbox{$\displaystyle \text{E}_A(0) \;=\; \text{Kern }\left(\begin{array}{rrr... ...nd{pmatrix},\begin{pmatrix}-2/3\\ 1/3\\ 0\\ 0\\ 1\end{pmatrix}\rangle\;. $}$

Gram-Schmidt ergibt für $ \mbox{$\text{E}_A(0)$}$ die Orthonormalbasis

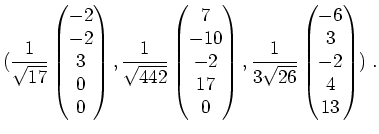
$ \mbox{$\displaystyle (\frac{1}{\sqrt{17}}\begin{pmatrix}-2\\ -2\\ 3\\ 0\\ ... ...\frac{1}{3\sqrt{26}}\begin{pmatrix}-6\\ 3\\ -2\\ 4\\ 13\end{pmatrix})\;. $}$

Ferner wird

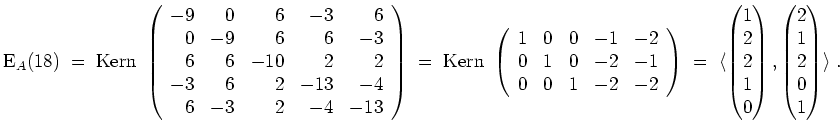
$ \mbox{$\displaystyle \text{E}_A(18) \;=\; \text{Kern }\left(\begin{array}{rr... ... 0\end{pmatrix},\begin{pmatrix}2\\ 1\\ 2\\ 0\\ 1\end{pmatrix}\rangle\;. $}$

Gram-Schmidt ergibt für $ \mbox{$\text{E}_A(18)$}$ die Orthonormalbasis

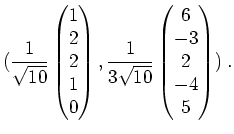
$ \mbox{$\displaystyle (\frac{1}{\sqrt{10}}\begin{pmatrix}1\\ 2\\ 2\\ 1\\ 0... ... \frac{1}{3\sqrt{10}}\begin{pmatrix}6\\ -3\\ 2\\ -4\\ 5\end{pmatrix})\;. $}$

Damit erhalten wir die unitäre Matrix

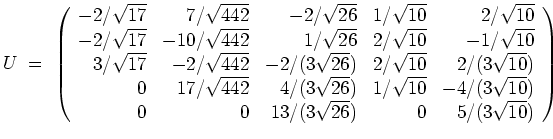
$ \mbox{$\displaystyle U \;=\; \left(\begin{array}{rrrrr} -2/\sqrt{17}& 7/\sq... ...10})\\ 0 & 0 & 13/(3\sqrt{26})& 0 & 5/(3\sqrt{10})\\ \end{array}\right) $}$

und somit

$ \mbox{$\displaystyle \bar{U}^\text{t} AU \;=\; \text{diag}(0,0,0,18,18)\;. $}$

Dieses Standardverfahren liefert i.a. nicht die einfachsten Zahlenwerte. Zum Beispiel ergibt sich auch mit

$ \mbox{$\displaystyle \tilde{U} \;=\; \frac{1}{6}\left(\begin{array}{rrrrr} ... ... 4& 0& 2& 0& 4\\ 1& 3& -4& -3& 1\\ 1& -3& -4& 3& 1 \end{array}\right) $}$
die unitäre Diagonalisierung

$ \mbox{$\displaystyle \overline{\tilde{U}}^{\;\text{t}} A\tilde{U} \;=\; \text{diag}(0,0,0,18,18)\;. $}$