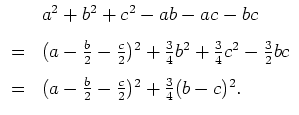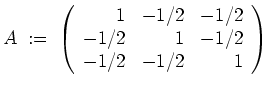
Mit
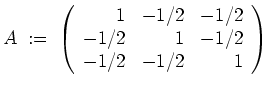
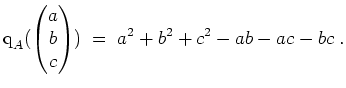
Es gilt also
![]() für alle
für alle
![]() genau dann, wenn
genau dann, wenn
![]() positiv semidefinit ist.
positiv semidefinit ist.
Beidseitiger Gaußscher Algorithmus liefert
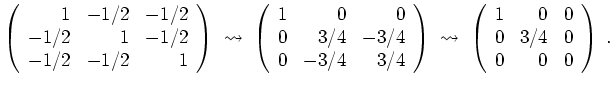
Damit ist
![]() in der Tat positiv semidefinit; genauer gesagt ist ihre Signatur
in der Tat positiv semidefinit; genauer gesagt ist ihre Signatur
![]() .
.
Alternativ bietet sich eine quadratische Ergänzung an. Es ist