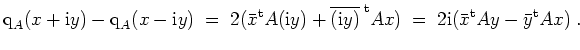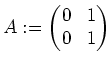
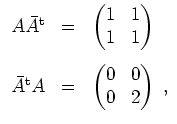
Man kann hierfür auch die Tatsache verwenden, daß eine normale obere Dreiecksmatrix notwendig eine Diagonalmatrix ist.
Wegen

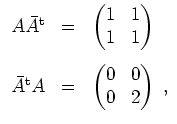
Man kann hierfür auch die Tatsache verwenden, daß eine normale obere Dreiecksmatrix notwendig eine Diagonalmatrix ist.
Wegen