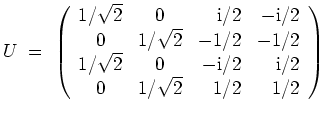Lösung.

Es wird

$ \mbox{$\displaystyle \bar{A}^\text{t} A \;=\; \left(\begin{array}{rrrr} 10 & ... ... & 10 & 0 \\ 0 & -6 & 0 & 10 \end{array}\right) \;=\; A\bar{A}^\text{t}\, $}$
d.h. $ \mbox{$A$}$ ist normal und damit unitär diagonalisierbar.

Das charakteristische Polynom ergibt sich zu

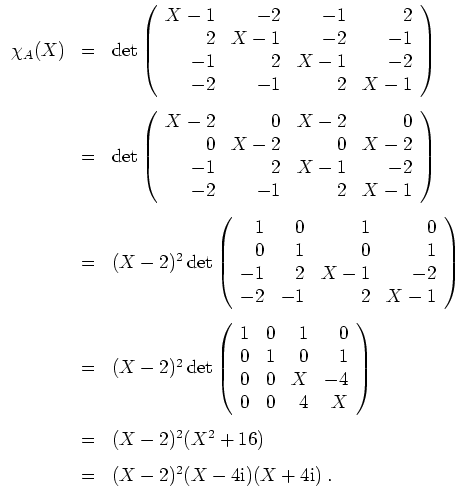
$ \mbox{$\displaystyle \begin{array}{rcl} \chi_A(X) &=& \det\left(\begin{array... ...)\vspace*{3mm} \\ &=& (X-2)^2 (X-4\mathrm{i})(X+4\mathrm{i})\;. \end{array}$}$

Also sind $ \mbox{$2$}$ , $ \mbox{$4\mathrm{i}$}$ und $ \mbox{$-4\mathrm{i}$}$ die Eigenwerte von $ \mbox{$A$}$ .

Die Eigenräume von $ \mbox{$A$}$ ergeben sich wie folgt.

Es wird

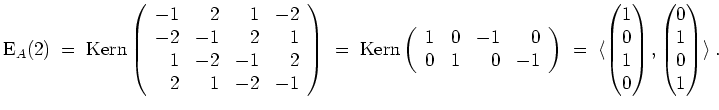
$ \mbox{$\displaystyle \text{E}_A(2) \;=\; \text{Kern}\left(\begin{array}{rrrr}... ... 1\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1\\ 0\\ 1\end{pmatrix}\rangle\;. $}$

Eine Orthonormalbasis von $ \mbox{$\text{E}_A(2)$}$ ergibt sich zu

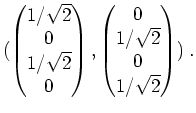
$ \mbox{$\displaystyle (\begin{pmatrix}1/\sqrt{2}\\ 0\\ 1/\sqrt{2}\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1/\sqrt{2}\\ 0\\ 1/\sqrt{2}\end{pmatrix})\;. $}$

Es wird

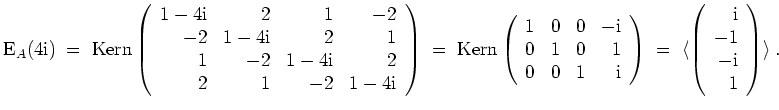
$ \mbox{$\displaystyle \text{E}_A(4\mathrm{i}) \;=\; \text{Kern}\left(\begin{ar... ...in{array}{r}\mathrm{i}\\ -1\\ -\mathrm{i}\\ 1\end{array}\right)\rangle\;. $}$

Eine Orthonormalbasis von $ \mbox{$\text{E}_A(4\mathrm{i})$}$ ergibt sich zu

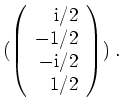
$ \mbox{$\displaystyle (\left(\begin{array}{r}\mathrm{i}/2\\ -1/2\\ -\mathrm{i}/2\\ 1/2\end{array}\right))\;. $}$

Es wird

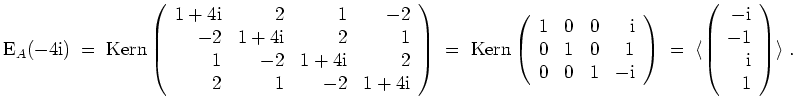
$ \mbox{$\displaystyle \text{E}_A(-4\mathrm{i}) \;=\; \text{Kern}\left(\begin{a... ...in{array}{r}-\mathrm{i}\\ -1\\ \mathrm{i}\\ 1\end{array}\right)\rangle\;. $}$

Eine Orthonormalbasis von $ \mbox{$\text{E}_A(-4\mathrm{i})$}$ ergibt sich zu

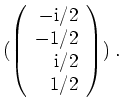
$ \mbox{$\displaystyle (\left(\begin{array}{r}-\mathrm{i}/2\\ -1/2\\ \mathrm{i}/2\\ 1/2\end{array}\right))\;. $}$

Zur Probe verifizieren wir, daß die Eigenräume bezüglich verschiedener Eigenräume in der Tat zueinander orthogonal sind.

Zusammengesetzt erhalten wir also mit

$ \mbox{$\displaystyle U \;=\; \left(\begin{array}{ccrr} 1/\sqrt{2} & 0 & \mat... ...i}/2 & \mathrm{i}/2 \\ 0 & 1/\sqrt{2} & 1/2 & 1/2 \\ \end{array}\right) $}$
die unitäre Diagonalisierung
$ \mbox{$\displaystyle \bar{U}^\text{t} A U \;=\; \text{diag}(2,2,4\mathrm{i},-4\mathrm{i})\; . $}$