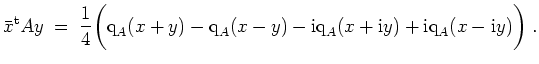Beispiel.

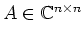Sei $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ .

1.
Zeige, daß aus 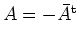$ \mbox{$A = -\bar{A}^\text{t}$}$ die unitäre Diagonalisierbarkeit von 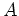$ \mbox{$A$}$ folgt.

2.
Gib eine Matrix 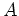$ \mbox{$A$}$ an, die diagonalisierbar, aber nicht unitär diagonalisierbar ist.

3.
Sei 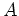$ \mbox{$A$}$ hermitesch. Zeige: Ist ein Diagonaleintrag von 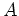$ \mbox{$A$}$ größer 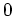$ \mbox{$0$}$ , und ein Diagonaleintrag von 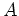$ \mbox{$A$}$ kleiner 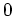$ \mbox{$0$}$ , so hat 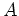$ \mbox{$A$}$ einen positiven und einen negativen Eigenwert.

4.
Zeige, daß für 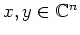$ \mbox{$x,y\in\mathbb{C}^n$}$ gilt:
$ \mbox{$\displaystyle \bar{x}^\text{t} Ay \;=\; \frac{1}{4}\bigg(\text{q}_A(x+... ...hrm{i}\text{q}_A(x+\mathrm{i}y)+\mathrm{i}\text{q}_A(x-\mathrm{i}y)\bigg)\;. $}$

5.
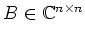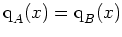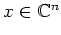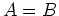Sei $ \mbox{$B\in\mathbb{C}^{n\times n}$}$ mit $ \mbox{$\text{q}_A(x)=\text{q}_B(x)$}$ für alle $ \mbox{$x\in\mathbb{C}^n$}$ . Zeige, daß $ \mbox{$A=B$}$ .

6.
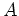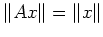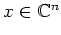Zeige: $ \mbox{$A$}$ ist unitär genau dann, wenn $ \mbox{$\Vert Ax\Vert=\Vert x\Vert$}$ für alle $ \mbox{$x\in\mathbb{C}^n$}$ .