Lösung.

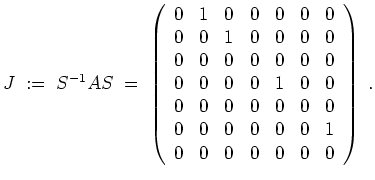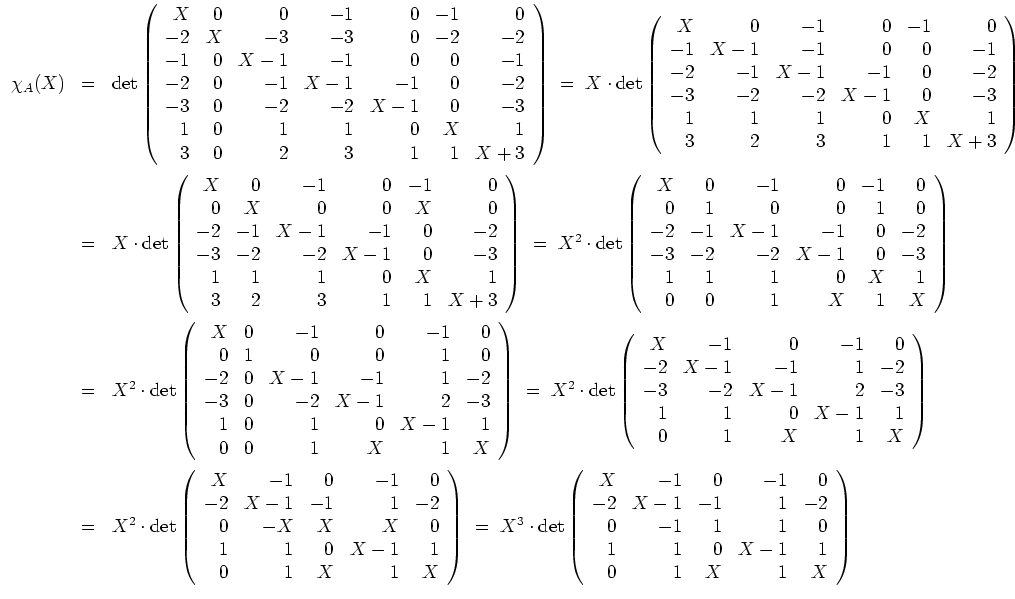
Es wird

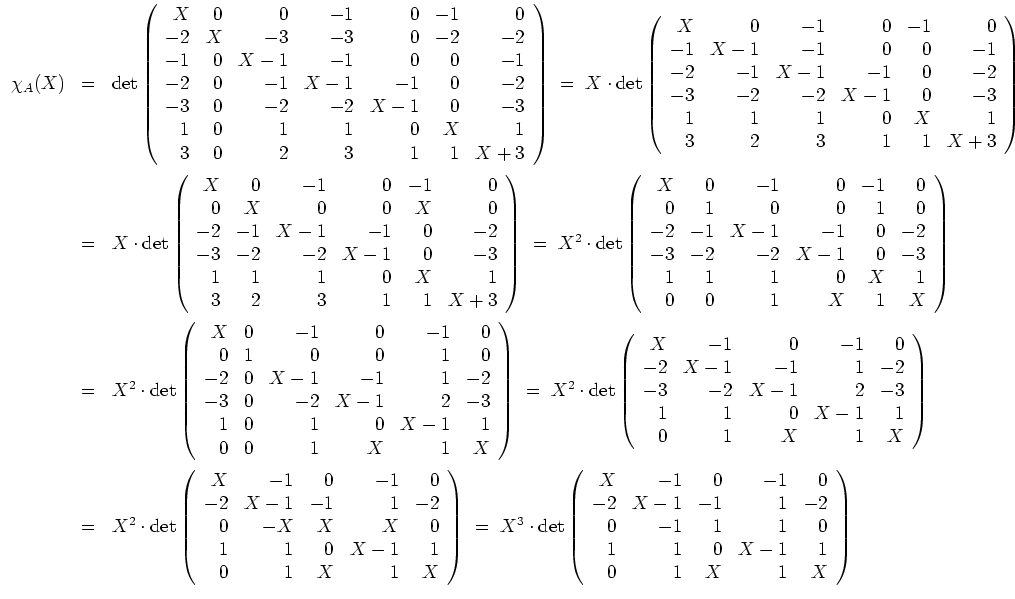
$ \mbox{$\displaystyle \begin{array}{rcl} \chi_A(X) & = & \det\left(\begin{arr... ...& 1 & 0 & X-1 & 1 \\ 0 & 1 & X & 1 & X \\ \end{array}\right) \end{array}$}$
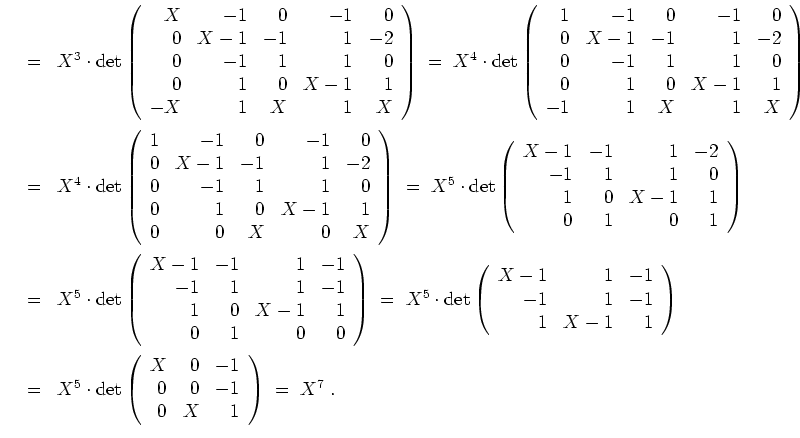
$ \mbox{$\displaystyle \begin{array}{rcl} &=& X^3\cdot\det\left(\begin{array}{r... ...0 & -1 \\ 0 & X & 1 \\ \end{array}\right) \;=\; X^7\; . \\ \end{array}$}$
Dies liefert einen Eigenwert $ \mbox{$0$}$ mit der algebraischen Vielfachheit eins.

Wenden wir den Algorithmus in formaler Schreibweise an. Es ist $ \mbox{$C = A$}$ .

Mit der Zeilenstufenform

$ \mbox{$\displaystyle Z_1 \; =\; \left( \begin{array}{rrrrrrr} 1 & 0 & 0 & 0 &... ...0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 2 & 0 \\ \end{array}\right) $}$
von $ \mbox{$C$}$ erhalten wir
$ \mbox{$\displaystyle \underline{y}_1 \; =\; ( \left( \begin{array}{r} 0 \\ ... ...y}{r} -1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ \end{array}\right) ) $}$
als eine Basis von $ \mbox{$\text{Kern}(C^1)$}$ .

Mit der Zeilenstufenform

$ \mbox{$\displaystyle Z_2 \; =\; \left( \begin{array}{rrrrrrr} 1 & 0 & 0 & 0 & 1 & 0 & 1 \\ \end{array}\right) $}$
von $ \mbox{$Z_1\cdot C$}$ (und damit auch von $ \mbox{$C^2$}$ ) erhalten wir
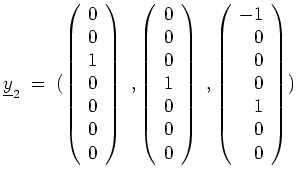
$ \mbox{$\displaystyle \underline{y}_2 \; =\; ( \left( \begin{array}{r} 0 \\ ... ...y}{r} -1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ \end{array}\right) ) $}$
als eine Basisergänzung von $ \mbox{$\text{Kern}(C^1)$}$ zu $ \mbox{$\text{Kern}(C^2)$}$ .

Nun ist $ \mbox{$Z_2\cdot C = 0$}$ . Damit erhalten wir

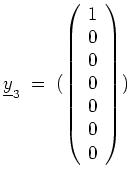
$ \mbox{$\displaystyle \underline{y}_3 \; =\; ( \left( \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right) ) $}$
als eine Basisergänzung von $ \mbox{$\text{Kern}(C^2)$}$ zu $ \mbox{$\text{Kern}(C^3) = \text{H}_A(0) = \mathbb{C}^7$}$ .

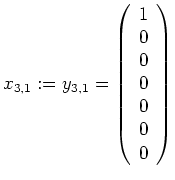In Stufe $ \mbox{$3$}$ nehmen wir $ \mbox{$x_{3,1} := y_{3,1} = \left( \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right)$}$ .

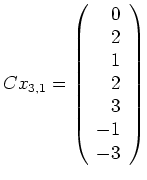In Stufe $ \mbox{$2$}$ ist zunächst $ \mbox{$C x_{3,1} = \left( \begin{array}{r} 0 \\ 2 \\ 1 \\ 2 \\ 3 \\ -1 \\ -3 \\ \end{array}\right)$}$ .

Da wir nun auf Augenschein hin keine Auswahl mehr treffen können, formen wir nun die Matrix $ \mbox{$(y_{1,1},y_{1,2},y_{1,3},C x_{3,1},y_{2,1},y_{2,2},y_{2,3})$}$ in die Zeilenstufenform

$ \mbox{$\displaystyle \left( \begin{array}{rrrrrrr} 1 & 0 & 0 & 0 & 0 & 0 & -... ...& 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right) $}$
Da hierin die letzte Spaltenposition nichtausgewählt ist, können unter Weglassen des letzten Vektors die Basis $ \mbox{$(y_{1,1},y_{1,2},y_{1,3},C x_{3,1},y_{2,1},y_{2,2})$}$ von $ \mbox{$\text{Kern}(C^2)$}$ auswählen und $ \mbox{$x_{2,1} := y_{2,1}$}$ und $ \mbox{$x_{2,2} := y_{2,2}$}$ .

(Man hätte auch $ \mbox{$y_{2,2}$}$ streichen können, nicht aber $ \mbox{$y_{2,1}$}$ , wie man dieser Zeilenstufenform ansehen kann.)

In Stufe $ \mbox{$1$}$ erhalten wir die Basis

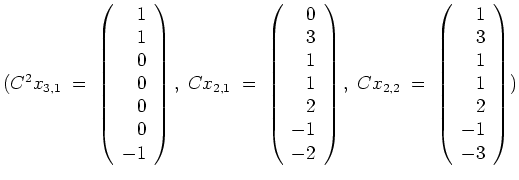
$ \mbox{$\displaystyle (C^2 x_{3,1}\; =\; \left( \begin{array}{r} 1 \\ 1 \\ ... ...}{r} 1 \\ 3 \\ 1 \\ 1 \\ 2 \\ -1 \\ -3 \\ \end{array}\right) ) $}$
von $ \mbox{$\text{Kern}(C^1)$}$ .

Wir setzen die Ketten $ \mbox{$(C^2 x_{3,1}, C x_{3,1}, x_{3,1})$}$ , $ \mbox{$(C x_{2,1}, x_{2,1})$}$ , $ \mbox{$(C x_{2,2}, X_{2,2})$}$ in die Matrix

$ \mbox{$\displaystyle S \; =\; \left( \begin{array}{rrrrrrr} 1 & 0 & 1 & 0 &... ... -1 & 0 & -1 & 0 \\ -1 & -3 & 0 & -2 & 0 & -3 & 0 \\ \end{array}\right) $}$
und erhalten
$ \mbox{$\displaystyle J \; := \; S^{-1}AS \; =\; \left( \begin{array}{rrrrrrr... ... & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right)\; . $}$
Zur Probe verifizieren wir noch, daß $ \mbox{$SJ = AS$}$ ist, und daß $ \mbox{$S$}$ invertierbar ist.