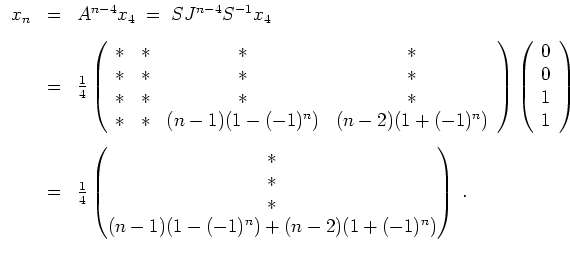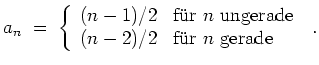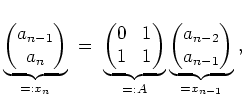
Wir erhalten
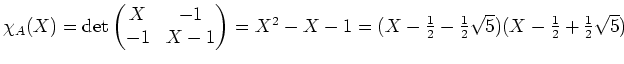 .
.
Es wird
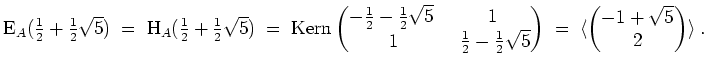
Ferner wird
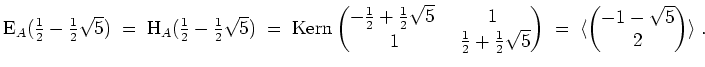
Mit
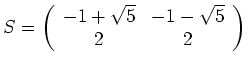 wird
wird
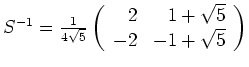 und
und
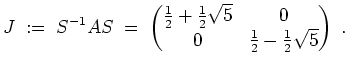
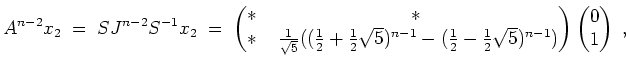
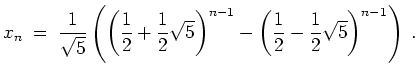
Wir erhalten
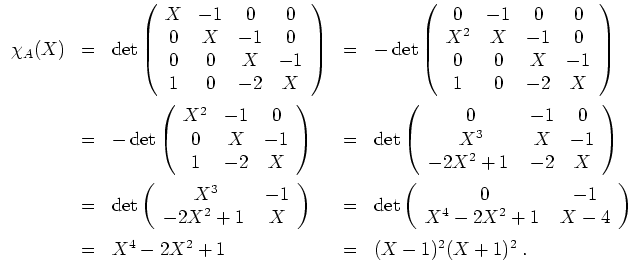
- (Eigenwert
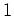 )
) - Wir bringen die Matrix
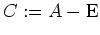 auf Zeilenstufenform und erhalten
Also ist eine Basis von
auf Zeilenstufenform und erhalten
Also ist eine Basis von
 gegeben durch
Nun bringen wir die Matrix
gegeben durch
Nun bringen wir die Matrix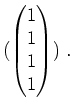
 auf Zeilenstufenform und erhalten
Also können wir die Basis von
auf Zeilenstufenform und erhalten
Also können wir die Basis von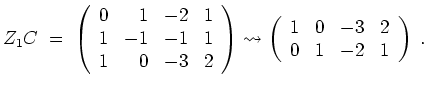
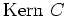 ergänzen zu einer Basis
von
ergänzen zu einer Basis
von
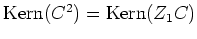 . Da die Dimension des Hauptraums
. Da die Dimension des Hauptraums
 mit der
Dimension von
mit der
Dimension von
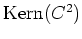 übereinstimmt, haben wir bereits eine Basis von
übereinstimmt, haben wir bereits eine Basis von
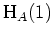 gefunden.
Das Tableau zu
gefunden.
Das Tableau zu
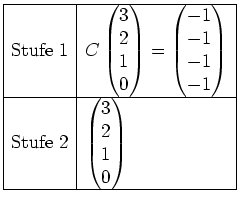
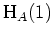 sieht vor der Kettenbildung also wie folgt aus.
Nun bilden wir den Vektor in Stufe
sieht vor der Kettenbildung also wie folgt aus.
Nun bilden wir den Vektor in Stufe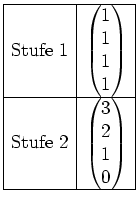
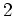 mittels
mittels
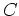 ab, tragen ihn in Stufe
ab, tragen ihn in Stufe
 ein, und streichen den schon vorhandenen
Vektor in Stufe
ein, und streichen den schon vorhandenen
Vektor in Stufe
 aus Dimensionsgründen.
aus Dimensionsgründen.
- (Eigenwert
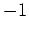 )
) - Wir bringen die Matrix
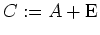 auf Zeilenstufenform und erhalten
Also ist eine Basis von
auf Zeilenstufenform und erhalten
Also ist eine Basis von
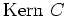 gegeben durch
Nun bringen wir die Matrix
gegeben durch
Nun bringen wir die Matrix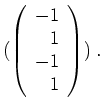
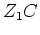 auf Zeilenstufenform und erhalten
Also können wir die Basis von
auf Zeilenstufenform und erhalten
Also können wir die Basis von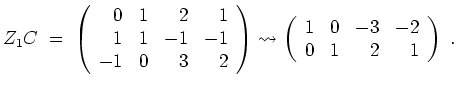
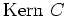 ergänzen zu einer Basis
von
ergänzen zu einer Basis
von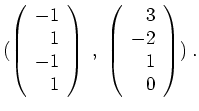
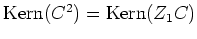 . Da die Dimension des Hauptraums
. Da die Dimension des Hauptraums
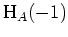 mit der
Dimension von
mit der
Dimension von
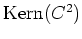 übereinstimmt, haben wir bereits eine Basis von
übereinstimmt, haben wir bereits eine Basis von
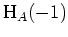 gefunden.
Das Tableau zu
gefunden.
Das Tableau zu
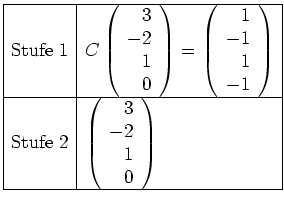
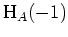 sieht vor der Kettenbildung also wie folgt aus.
Nun bilden wir den Vektor in Stufe
sieht vor der Kettenbildung also wie folgt aus.
Nun bilden wir den Vektor in Stufe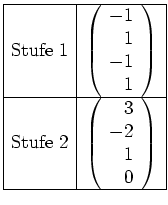
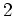 mittels
mittels
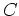 ab, tragen ihn in Stufe
ab, tragen ihn in Stufe
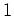 ein, und streichen den schon vorhandenen
Vektor in Stufe
ein, und streichen den schon vorhandenen
Vektor in Stufe
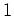 aus Dimensionsgründen.
aus Dimensionsgründen.
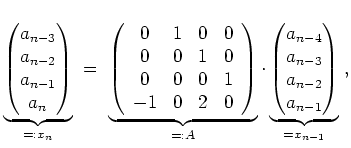
Nun können wir die beiden Kettenbasen als Spalten in die Matrix
![]() eintragen.
eintragen.
Mit
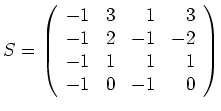 wird
wird
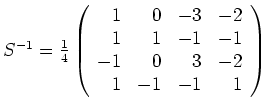 und
und
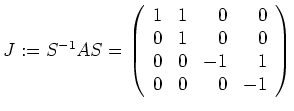 .
.
Da nun
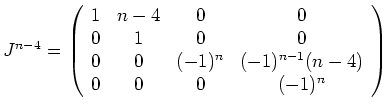 , wird
, wird