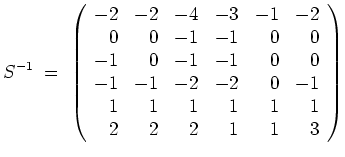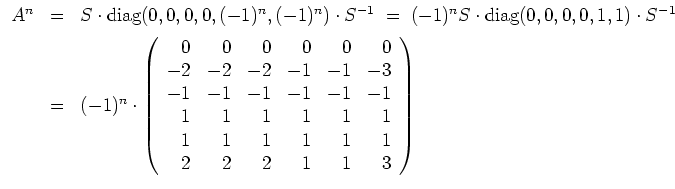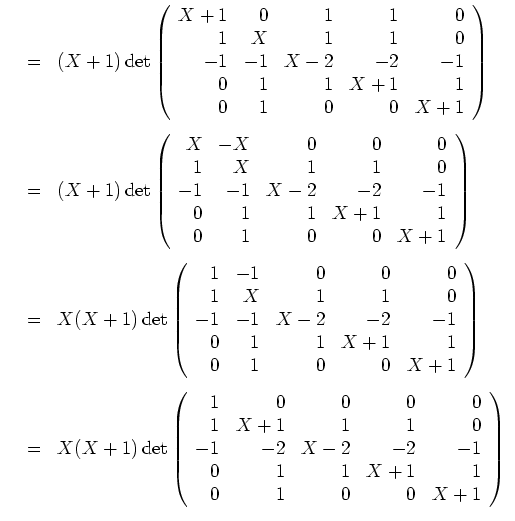
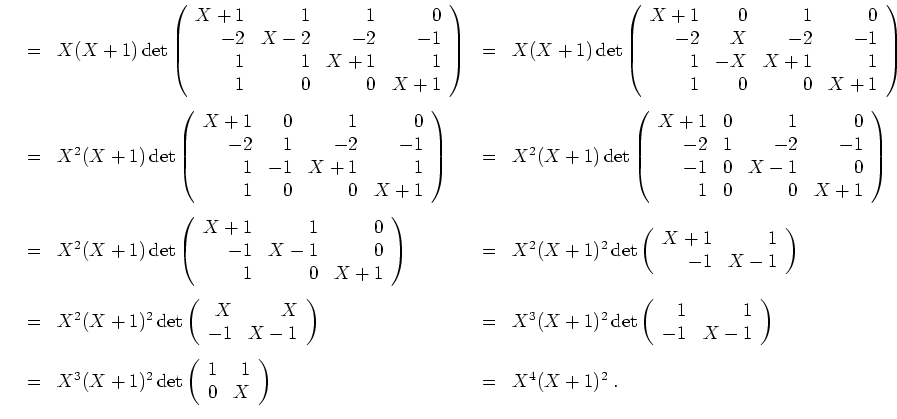
Die Eigenwerte von
![]() sind
sind
![]() mit algebraischer Vielfachheit vier und
mit algebraischer Vielfachheit vier und
![]() mit algebraischer Vielfachheit zwei.
mit algebraischer Vielfachheit zwei.
- (Eigenwert
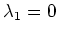 )
) - Wir bringen
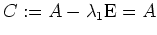 auf Zeilenstufenform (inklusive Streichens von Nullzeilen)
auf Zeilenstufenform (inklusive Streichens von Nullzeilen)

Wir erhalten als Basis von
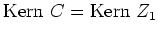

Nun bringen wir
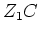 auf Zeilenstufenform
Position
auf Zeilenstufenform
Position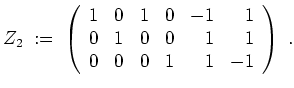
 ist eine neu hinzugekommene nichtausgewählte Spaltenposition. Wir können also die Basis
von
ist eine neu hinzugekommene nichtausgewählte Spaltenposition. Wir können also die Basis
von
 ergänzen zu einer Basis von
ergänzen zu einer Basis von

Nun bringen wir
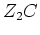 auf Zeilenstufenform
Position
auf Zeilenstufenform
Position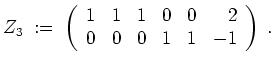
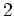 ist eine neu hinzugekommene nichtausgewählte Spaltenposition.
Wir können also die Basis von
ist eine neu hinzugekommene nichtausgewählte Spaltenposition.
Wir können also die Basis von
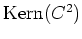 ergänzen zu einer Basis von
ergänzen zu einer Basis von
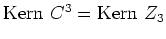 Nun ist
Nun ist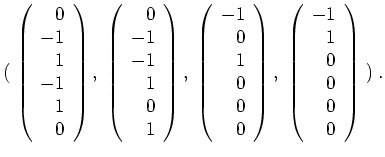
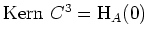 , da seine Dimension gleich der algebraischen Vielfachheit von
, da seine Dimension gleich der algebraischen Vielfachheit von
 als Eigenwert von
als Eigenwert von
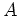 ist,
nämlich gleich
ist,
nämlich gleich
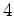 .
.
Das Tableau zu
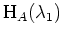 sieht also vor der Kettenbildung wie folgt aus.
Nun bilden wir den Vektor in Stufe
sieht also vor der Kettenbildung wie folgt aus.
Nun bilden wir den Vektor in Stufe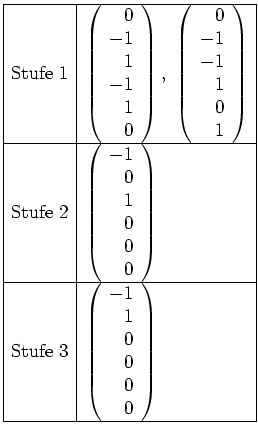
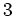 mittels
mittels
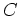 ab, tragen ihn in Stufe
ab, tragen ihn in Stufe
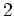 ein, und streichen den bereits
vorhanden Vektor in Stufe
ein, und streichen den bereits
vorhanden Vektor in Stufe
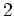 aus Dimensionsgründen.
Nun bilden wir den Vektor in Stufe
aus Dimensionsgründen.
Nun bilden wir den Vektor in Stufe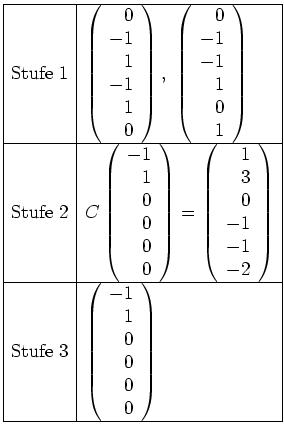
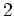 mittels
mittels
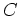 ab, tragen ihn in Stufe
ab, tragen ihn in Stufe
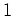 ein, und streichen den zweiten
der schon vorhandenen Vektoren in Stufe
ein, und streichen den zweiten
der schon vorhandenen Vektoren in Stufe
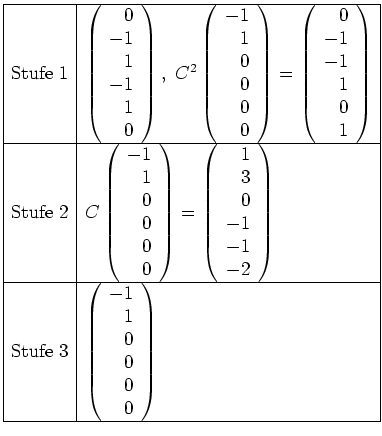
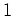 (der zufälligerweise mit dem neu eingetragenen Vektor identisch ist).
Abschließend sieht unser Tableau also wie folgt aus.
(der zufälligerweise mit dem neu eingetragenen Vektor identisch ist).
Abschließend sieht unser Tableau also wie folgt aus.
- (Eigenwert
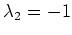 )
) - Wir bringen
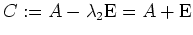 auf Zeilenstufenform
Wir erhalten als Basis von
auf Zeilenstufenform
Wir erhalten als Basis von
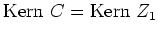 Nun ist
Nun ist
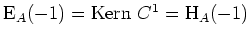 , da seine Dimension gleich der algebraischen Vielfachheit von
, da seine Dimension gleich der algebraischen Vielfachheit von
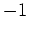 als
Eigenwert von
als
Eigenwert von
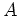 ist, nämlich gleich
ist, nämlich gleich
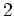 .
.
Das Tabelau zum Hauptraum
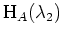 sieht also wie folgt aus.
Der zweite Schritt, die Kettenbildung, entfällt hier.
sieht also wie folgt aus.
Der zweite Schritt, die Kettenbildung, entfällt hier.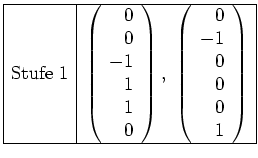
Zusammensetzen der Bestandteile liefert die Kettenbasis von
![]() , und somit
, und somit


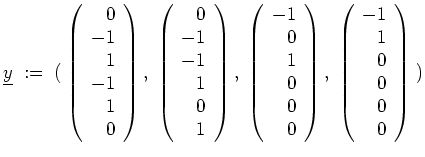
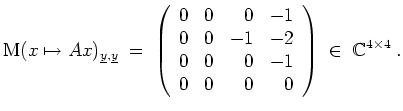
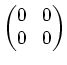 ,
,