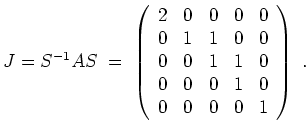Das charakteristische Polynom berechnet sich zu
Wir erhalten so die Eigenwerte
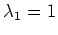 mit der algebraischen Vielfachheit
mit der algebraischen Vielfachheit
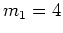 und
und
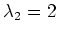 mit der algebraischen Vielfachheit
mit der algebraischen Vielfachheit
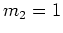 .
.
Im folgenden verwenden wir die formale Schreibweise des Algorithmus.
Beginnen wir mit
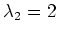 . Es ist hier
. Es ist hier
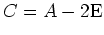 . Mit der Zeilenstufenform
. Mit der Zeilenstufenform
von
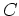 erhalten wir
als eine Basis von
erhalten wir
als eine Basis von
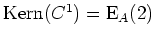 . Da die Dimension dieses Eigenraums gleich der algebraischen Vielfachheit ist, können wir sogleich den gefundenen Vektor
. Da die Dimension dieses Eigenraums gleich der algebraischen Vielfachheit ist, können wir sogleich den gefundenen Vektor
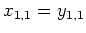 als einzigen Eintrag der Kette
als einzigen Eintrag der Kette
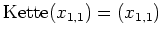 in die Matrix
in die Matrix
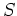 eintragen.
eintragen.
Fahren wir mit
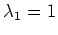 fort. Es ist hier
fort. Es ist hier
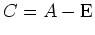 . Mit der Zeilenstufenform
. Mit der Zeilenstufenform
von
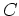 erhalten wir
als eine Basis von
erhalten wir
als eine Basis von
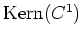 . Mit der Zeilenstufenform
von
. Mit der Zeilenstufenform
von
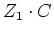 (und damit auch von
(und damit auch von
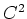 ) erhalten wir
als eine Basisergänzung von
) erhalten wir
als eine Basisergänzung von
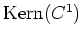 zu
zu
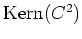 . Mit der Zeilenstufenform
von
. Mit der Zeilenstufenform
von
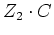 (und damit auch von
(und damit auch von
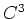 ) erhalten wir
als eine Basisergänzung von
) erhalten wir
als eine Basisergänzung von
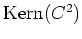 zu
zu
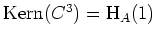 .
.
In Stufe
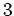 nehmen wir
nehmen wir
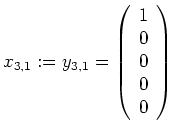 .
.
In Stufe
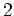 ist nun zunächst
ist nun zunächst
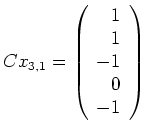 . Die aus
. Die aus
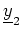 zu treffende Auswahl ist leer.
zu treffende Auswahl ist leer.
In Stufe
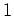 ist nun zunächst
ist nun zunächst
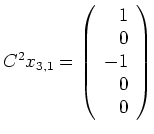 , so daß wir aus
, so daß wir aus
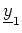 den Vektor
den Vektor
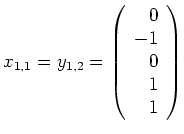 auswählen können (nicht aber
auswählen können (nicht aber
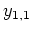 !). Tragen wir nun noch die Ketten
!). Tragen wir nun noch die Ketten
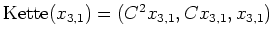 und
und
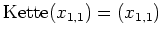 in die Matrix
in die Matrix
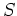 ein.
ein.
Wir erhalten
so erhalten wir entsprechend (ohne dafür
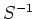 berechnen zu müssen)
Zur Probe verifizieren wir stattdessen, daß
berechnen zu müssen)
Zur Probe verifizieren wir stattdessen, daß
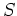 invertierbar ist, und daß
invertierbar ist, und daß
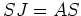 .
.
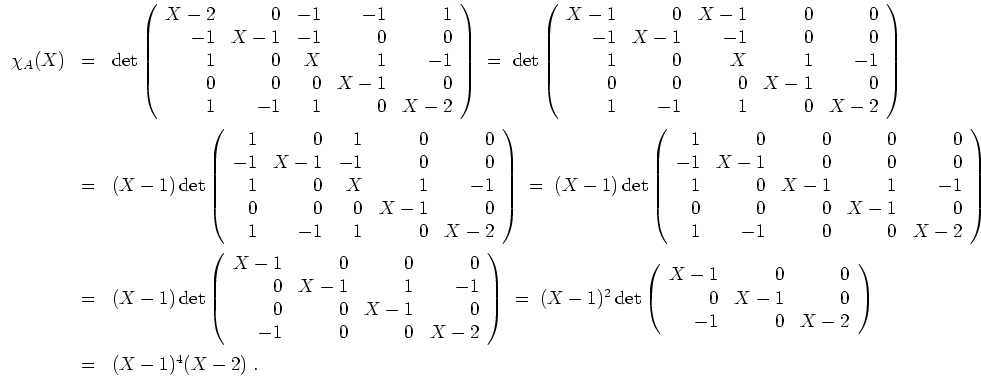
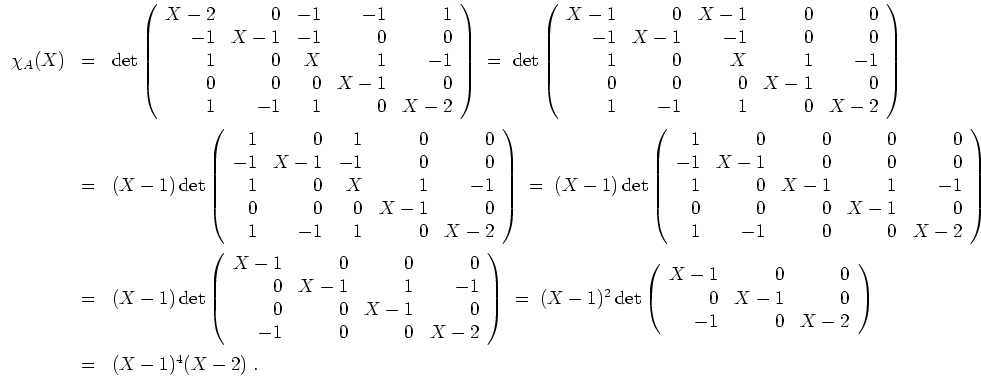
![]() . Es ist hier
. Es ist hier
![]() . Mit der Zeilenstufenform
. Mit der Zeilenstufenform
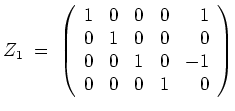
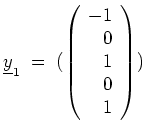
![]() fort. Es ist hier
fort. Es ist hier
![]() . Mit der Zeilenstufenform
. Mit der Zeilenstufenform

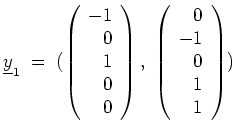
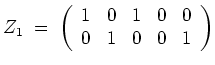
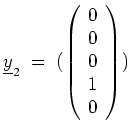
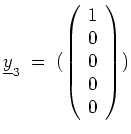
![]() nehmen wir
nehmen wir
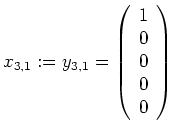 .
.
![]() ist nun zunächst
ist nun zunächst
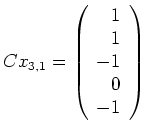 . Die aus
. Die aus
![]() zu treffende Auswahl ist leer.
zu treffende Auswahl ist leer.
![]() ist nun zunächst
ist nun zunächst
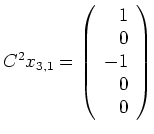 , so daß wir aus
, so daß wir aus
![]() den Vektor
den Vektor
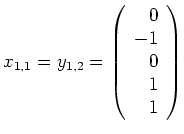 auswählen können (nicht aber
auswählen können (nicht aber
![]() !). Tragen wir nun noch die Ketten
!). Tragen wir nun noch die Ketten
![]() und
und
![]() in die Matrix
in die Matrix
![]() ein.
ein.