Lösung.

Sei invertierbar mit in Jordanform.

1.

Sei zunächst . Es ist und folglich für jeden auftretenden Jordanblock . Die Hauptdiagonaleinträge von sind alle gleich . Aus folgt nun . Da dies für jeden auftretenden Jordanblock gilt, ist der einzige Eigenwert.

Sei nun umgekehrt einziger Eigenwert von . Dann sind alle auftretenden Jordanblöcke der Form für gewisse , und es ist . Sei die maximale Kantenlänge aller auftretenden Jordanblöcke. Dann ist , und es folgt .

Alternativ ist für ein genau dann, wenn für ein , was wiederum genau dann gilt, wenn einziger Eigenwert von ist.

2.

Die Matrix ist diagonalisierbar genau dann, wenn eine Diagonalmatrix ist, was genau dann der Fall ist, wenn alle Jordanblöcke die Kantenlänge eins haben, was schließlich genau dann der Fall ist, wenn nur einfache Nullstellen hat.

3.

Sei und , wobei paarweise verschieden seien. Es ist die Summe der Kantenlängen aller Jordanblöcke zum Eigenwert gleich .

Daher ist genau dann, wenn ist für alle , was genau dann der Fall ist, wenn für jedes genau ein Jordanblock existiert, und zwar mit Kantenlänge , was schließlich dazu äquivalent ist, daß jeder Eigenwert geometrische Vielfachheit eins besitzt.

4.

Aus folgt . Träte in ein Jordanblock mit auf, so wäre . Auf der ersten oberen Nebendiagonalen von findet sich der Eintrag , wie eine Induktion zeigt. Aus folgt nun . Nun steht aber in der Hauptdiagonalen von eine Null, im Widerspruch zu . Also haben alle Jordanblöcke Kantenlänge eins, und es folgt diagonalisierbar.

Alternativ, mit gilt . Daher ist ein Teiler von . Die Nullstellen von sind genau die -ten Einheitswurzeln für , und diese sind paarweise verschieden. Es folgt . Also besitzt und somit auch nur einfache Nullstellen, und folglich ist diagonalisierbar.

5.

Mit ist . Somit ist oder . Im Falle ist wegen mithin . Im Falle hat eine doppelte Nullstelle, und daher ist dann nicht diagonalisierbar.

Zum Beispiel erfüllt die Matrix 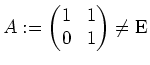die Gleichung .