Lösung.

Wir berechnen zunächst das charakteristische Polynom von $ \mbox{$A$}$ .

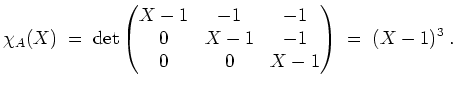
$ \mbox{$\displaystyle \chi_A(X) \;=\; \det\begin{pmatrix}X-1&-1&-1\\ 0&X-1&-1\\ 0&0&X-1\end{pmatrix} \;=\; (X-1)^3\;. $}$

Damit haben wir einen Eigenwert $ \mbox{$\lambda=1$}$ mit algebraischer Vielfachheit $ \mbox{$3$}$ .

Zur Berechnung der Matrizen $ \mbox{$S$}$ und $ \mbox{$J$}$ setzen wir

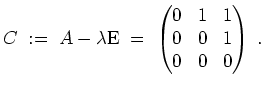
$ \mbox{$\displaystyle C \;:=\; A-\lambda\text{E} \;=\; \begin{pmatrix}0&1&1\\ 0&0&1\\ 0&0&0\end{pmatrix} \;. $}$

Der zugehörige Eigenraum ergibt sich zu

$ \mbox{$\displaystyle \text{E}_A(1) \;=\; \text{Kern }C \;=\; \text{Kern }\beg... ...\end{pmatrix} \;=\; \langle\begin{pmatrix}1\\ 0\\ 0\end{pmatrix}\rangle\;. $}$

Die geometrische Vielfachheit des Eigenwerts $ \mbox{$1$}$ ist somit $ \mbox{$\dim\text{E}_A(1)=1$}$ .

Die Matrix $ \mbox{$A$}$ ist nicht diagonalisierbar, denn die geometrische Vielfachheit des Eigenwerts ist kleiner als seine algebraische Vielfachheit.

Weiter wird

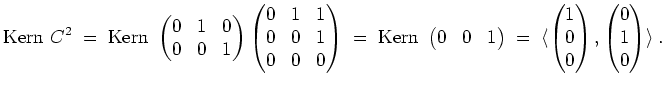
$ \mbox{$\displaystyle \text{Kern }C^2 \;=\; \text{Kern } \begin{pmatrix}0&1&0\... ...x}1\\ 0\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1\\ 0\end{pmatrix}\rangle\;. $}$

Schließlich wird

$ \mbox{$\displaystyle \text{Kern }C^3 \;=\; \text{Kern }\begin{pmatrix}0&0&1\e... ...atrix},\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\rangle \;=\; \text{H}_A(1)\;. $}$

Also sieht unser Tableau vor der Bildung von Ketten wie folgt aus.

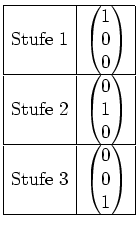
$ \mbox{$\displaystyle \begin{array}{\vert l\vert l\vert}\hline \text{Stufe } 1... ...ext{Stufe } 3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\\ \hline \end{array}$}$

Nun bilden wir alle Vektoren in Stufe $ \mbox{$3$}$ mittels der Matrix $ \mbox{$C$}$ ab, fügen sie in Stufe $ \mbox{$2$}$ ein, und streichen von den schon vorhandenen Vektoren in Stufe $ \mbox{$2$}$ eine geeignete Auswahl, so daß das Tableau weiterhin in Stufe $ \mbox{$1$}$ und Stufe $ \mbox{$2$}$ eine Basis von $ \mbox{$\text{Kern}(C^2)$}$ enthält. In diesem Fall muß aus Dimensionsgründen der schon vorhandene Vektor aus Stufe $ \mbox{$2$}$ gestrichen werden.

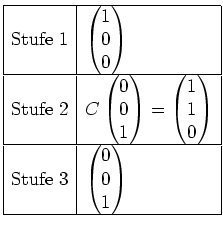
$ \mbox{$\displaystyle \begin{array}{\vert l\vert l\vert}\hline \par \text{Stuf... ...xt{Stufe } 3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix} \\ \hline \end{array}$}$

Schließlich bilden wir alle Vektoren in Stufe $ \mbox{$2$}$ mittels der Matrix $ \mbox{$C$}$ ab, fügen sie in Stufe $ \mbox{$1$}$ ein, und streichen von den schon vorhandenen Vektoren in Stufe $ \mbox{$1$}$ eine geeignete Auswahl, so daß das Tableau weiterhin in Stufe $ \mbox{$1$}$ eine Basis von $ \mbox{$\text{Kern }C$}$ enthält. Wiederum muß aus Dimensionsgründen der schon vorhandene Vektor aus Stufe $ \mbox{$1$}$ gestrichen werden. Also sieht unser Tableau letztlich wie folgt aus.

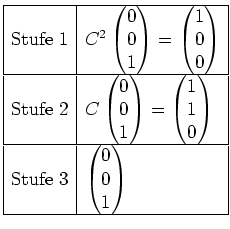
$ \mbox{$\displaystyle \begin{array}{\vert l\vert l\vert}\hline \text{Stufe } 1... ...ext{Stufe } 3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\\ \hline \end{array}$}$

Also besteht die Basis von $ \mbox{$\text{H}_A(1)=\mathbb{C}^3$}$ aus einer Kette. Trägt man diese Basis als Spalten in die Matrix

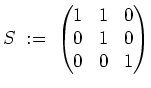
$ \mbox{$\displaystyle S \;:=\; \begin{pmatrix}1&1&0\\ 0&1&0\\ 0&0&1\end{pmatrix}$}$
ein, so erhält man die Jordanform
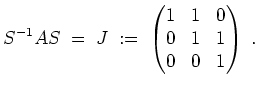
$ \mbox{$\displaystyle S^{-1}AS \;=\; J \;:=\; \begin{pmatrix}1&1&0\\ 0&1&1\\ 0&0&1\end{pmatrix} \;. $}$

Anstatt $ \mbox{$S^{-1}AS$}$ tatsächlich zu berechnen, rechnen wir zur Probe

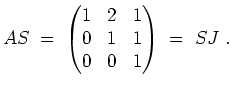
$ \mbox{$\displaystyle AS \;=\; \begin{pmatrix}1&2&1\\ 0&1&1\\ 0&0&1\end{pmatrix} \;=\; SJ \;. $}$

Das Minimalpolynom ist

$ \mbox{$\displaystyle \mu_A(X) \;=\; (X-1)^3\;, $}$
da die maximale Kantenlänge eines Jordanblocks zum Eigenwert $ \mbox{$1$}$ gleich $ \mbox{$3$}$ ist.