Sei
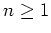 und
und
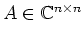 . Zeige folgende Aussagen.
. Zeige folgende Aussagen.
- 1.
- Es gibt ein
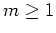 mit
mit
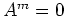 genau dann, wenn
genau dann, wenn
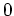 einziger Eigenwert von
einziger Eigenwert von
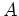 ist.
ist.
- 2.
- Die Matrix
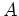 ist diagonalisierbar genau dann, wenn
ist diagonalisierbar genau dann, wenn
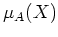 nur einfache Nullstellen besitzt, d.h. wenn
nur einfache Nullstellen besitzt, d.h. wenn
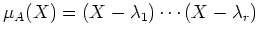 mit paarweise verschiedenen
mit paarweise verschiedenen
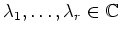 .
.
- 3.
- Es ist
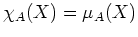 genau dann, wenn die geometrische Vielfachheit aller Eigenwerte gleich
genau dann, wenn die geometrische Vielfachheit aller Eigenwerte gleich
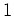 ist.
ist.
- 4.
- Ist
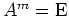 für ein
für ein
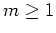 , so ist
, so ist
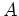 diagonalisierbar.
diagonalisierbar.
- 5.
- Ist
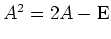 , so ist
, so ist
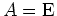 oder
oder
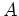 ist nicht diagonalisierbar. Gib ein Beispiel für den letzteren Fall an.
ist nicht diagonalisierbar. Gib ein Beispiel für den letzteren Fall an.
![]() und
und
![]() . Zeige folgende Aussagen.
. Zeige folgende Aussagen.