Lösung.

1.
Wir berechnen
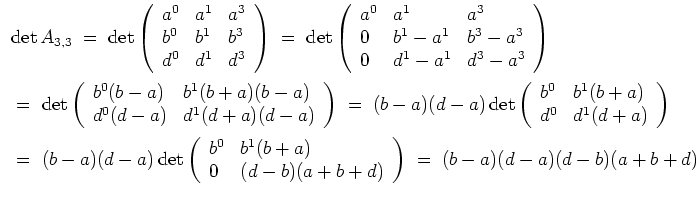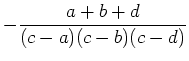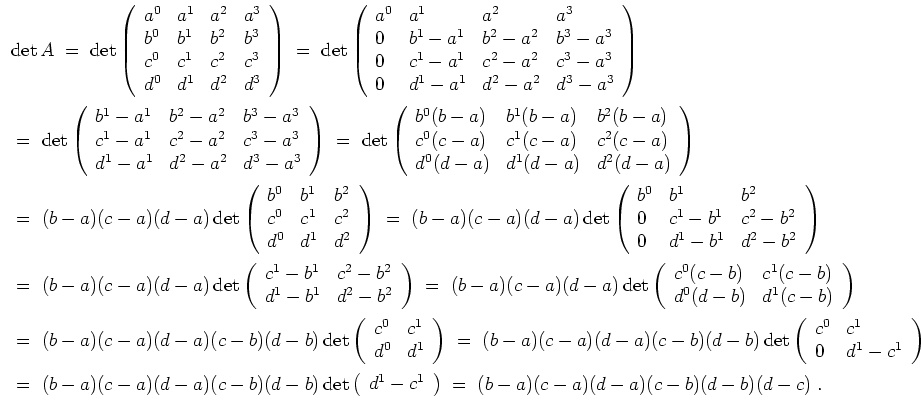
$ \mbox{$\displaystyle \begin{array}{l} \det A \;=\;\det\left(\begin{array}{lll... ...\right) \;=\; (b - a)(c - a)(d - a)(c - b)(d - b)(d - c)\; . \\ \end{array}$}$
Dies ist ein Beispiel einer Vandermondeschen Determinanten.

Es folgt aus der Determinante, daß $ \mbox{$A$}$ genau dann invertierbar ist, wenn $ \mbox{$a$}$ , $ \mbox{$b$}$ , $ \mbox{$c$}$ und $ \mbox{$d$}$ paarweise verschieden sind.

Hier ist ein alternatives Argument. Sind zwei Elemente aus $ \mbox{$(a,b,c,d)$}$ gleich, so hat $ \mbox{$A$}$ zwei gleiche Zeilen und ist singulär.

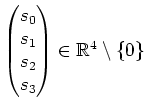Umgekehrt, seien die Einträge in $ \mbox{$(a,b,c,d)$}$ paarweise verschieden. Angenommen, $ \mbox{$A$}$ würde den Vektor $ \mbox{$\begin{pmatrix}s_0\\ s_1\\ s_2\\ s_3\end{pmatrix}\in\mathbb{R}^4\setminus\{ 0\}$}$ annullieren. Dann wäre $ \mbox{$s_0 X^0 + s_1 X^1 + s_2 X^2 + s_3 X^3$}$ ein nichtverschwindendes Polynom von Grad $ \mbox{$\le 3$}$ , welches vier verschiedene Nullstellen hat. Das gibt es nicht, und damit ist die Annahme als falsch nachgewiesen. Also ist $ \mbox{$\text{Kern }A = \{0\}$}$ , und mithin $ \mbox{$A$}$ regulär.

2.
Mit der Cramerschen Regel berechnen wir zunächst
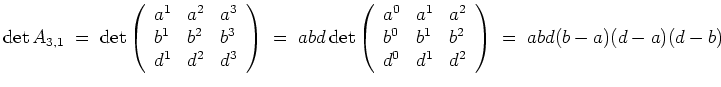
$ \mbox{$\displaystyle \det A_{3,1} \;=\; \det \left(\begin{array}{lll} a^1 &... ...\\ d^0 & d^1 & d^2 \\ \end{array}\right) \;=\; abd(b - a)(d - a)(d - b) $}$
und erhalten den Eintrag
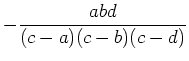
$ \mbox{$\displaystyle -\frac{abd}{(c - a)(c - b)(c - d)} $}$
an Position $ \mbox{$(1,3)$}$ von $ \mbox{$A^{-1}$}$ .

Ähnlich berechnen wir

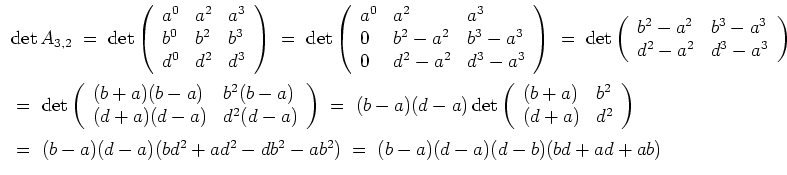
$ \mbox{$\displaystyle \begin{array}{l} \det A_{3,2} \;=\; \det \left(\begin{a... ... + ad^2 - db^2 - ab^2) \;=\; (b - a)(d - a)(d - b)(bd + ad + ab) \end{array}$}$
und erhalten den Eintrag
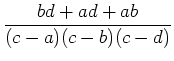
$ \mbox{$\displaystyle \frac{bd + ad + ab}{(c - a)(c - b)(c - d)} $}$
an Position $ \mbox{$(2,3)$}$ von $ \mbox{$A^{-1}$}$ .

Schließlich berechnen wir

$ \mbox{$\displaystyle \begin{array}{l} \det A_{3,3} \;=\; \det \left(\begin{a... ... d)\\ \end{array}\right) \;=\; (b - a)(d - a)(d - b)(a + b + d) \end{array}$}$
und erhalten den Eintrag
$ \mbox{$\displaystyle - \frac{a + b + d}{(c - a)(c - b)(c - d)} $}$
an Position $ \mbox{$(3,3)$}$ von $ \mbox{$A^{-1}$}$ .