Seien
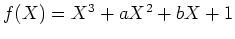 und
und
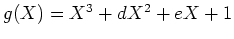 reelle Polynome.
reelle Polynome.
- 1.
- Zeige, daß
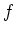 und
und
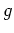 genau dann einer Gleichung (Gleichheit von Polynomen) der Form
für gewisse reellen Polynome
genau dann einer Gleichung (Gleichheit von Polynomen) der Form
für gewisse reellen Polynome
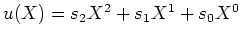 und
und
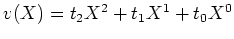 , die nicht beide verschwinden sollen, genügen, wenn
Diese Matrix heißt auch Sylvestersche Matrix, und ihre Determinante die Resultante der Polynome
, die nicht beide verschwinden sollen, genügen, wenn
Diese Matrix heißt auch Sylvestersche Matrix, und ihre Determinante die Resultante der Polynome
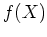 und
und
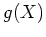 .
.
- 2.
- Berechne die Resultante von
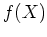 und
und
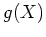 .
.
- 3.
- Zeige, daß die Resultante von
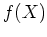 und
und
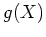 genau dann verschwindet, wenn ein Polynom
genau dann verschwindet, wenn ein Polynom
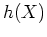 von Grad
von Grad
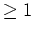 existiert, welches
existiert, welches
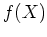 und
und
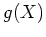 teilt.
Hierbei teile ein Polynom ein anderes, falls ersteres in einer Produktzerlegung letzterens auftritt.
teilt.
Hierbei teile ein Polynom ein anderes, falls ersteres in einer Produktzerlegung letzterens auftritt.
![]() und
und
![]() reelle Polynome.
reelle Polynome.
