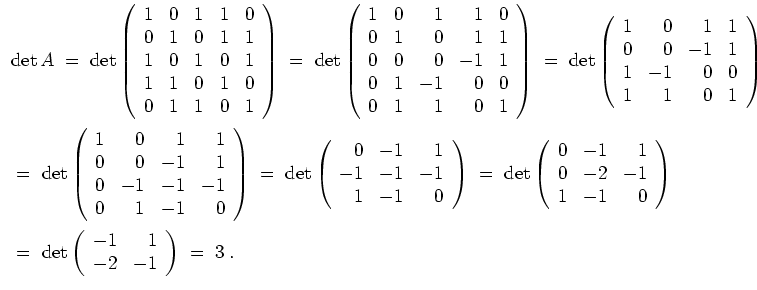
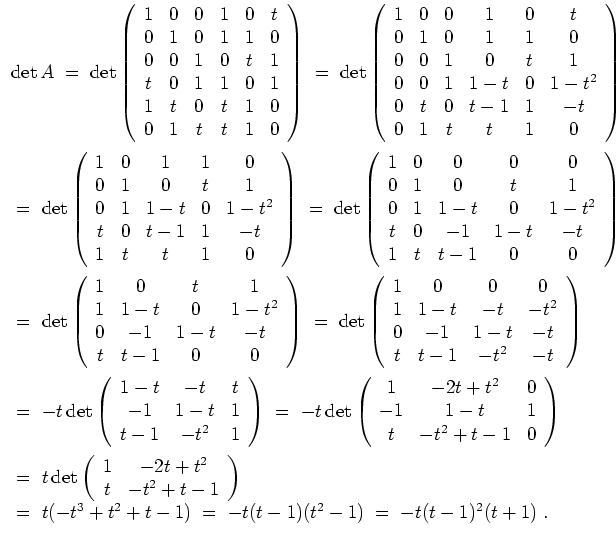
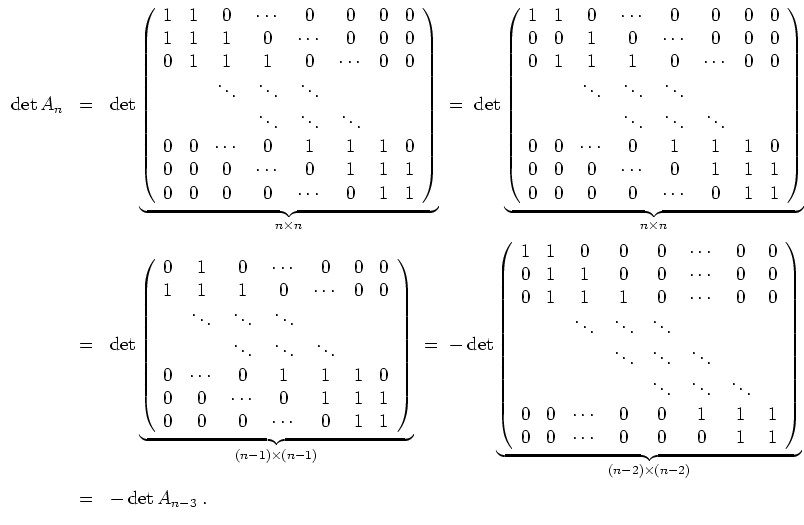
Wir erhalten somit folgendes Ergebnis. Sei
![]() der Rest von
der Rest von
![]() geteilt durch
geteilt durch
![]() ,
d.h.
,
d.h.
![]() für ein
für ein
![]() .
.
Falls
![]() , so ist
, so ist
![]() .
.
Falls
![]() , so ist
, so ist
![]() .
.
Falls
![]() , so ist
, so ist
![]() .
.
Damit ist
![]() singulär genau dann, wenn
singulär genau dann, wenn
![]() liegt (man schreibt auch: wenn
liegt (man schreibt auch: wenn
![]() oder
oder
![]() ).
).