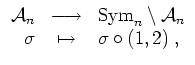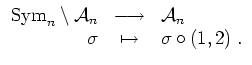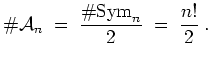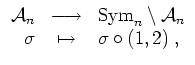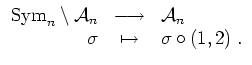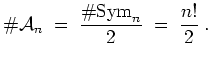- 1.
- Wir erhalten
Das Element der ersten Zeile hat Vorzeichen
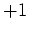 . Die Elemente der zweiten Zeile haben Vorzeichen
. Die Elemente der zweiten Zeile haben Vorzeichen
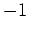 .
Die Elemente der dritten Zeile haben Vorzeichen
.
Die Elemente der dritten Zeile haben Vorzeichen
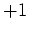 . Die Elemente der vierten Zeile haben Vorzeichen
. Die Elemente der vierten Zeile haben Vorzeichen
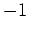 .
Die Elemente der fünften Zeile haben Vorzeichen
.
Die Elemente der fünften Zeile haben Vorzeichen
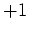 .
.
- 2.
- Sei
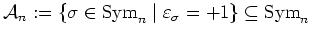 die Teilmenge
der Permutationen positiven Vorzeichens. Es gibt wegen
die Teilmenge
der Permutationen positiven Vorzeichens. Es gibt wegen
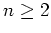 eine Bijektion
mit der Umkehrabbildung
In der Tat sind wegen
eine Bijektion
mit der Umkehrabbildung
In der Tat sind wegen
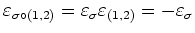 beide Abbildungen
wohldefiniert.
beide Abbildungen
wohldefiniert.
Damit ist