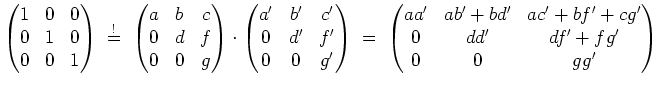
Die Gleichungen
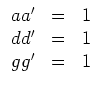
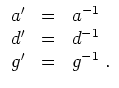
Dann liefern die Gleichungen
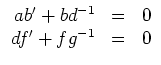
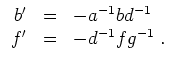
Schließlich folgt aus
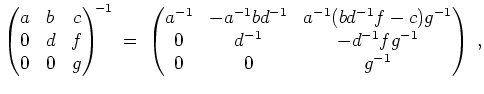
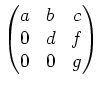 verifiziert.
verifiziert.
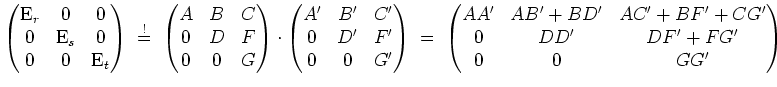
Die Gleichungen
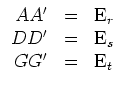
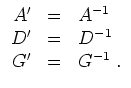
Dann liefern die Gleichungen
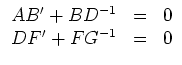
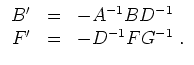
Schließlich folgt aus
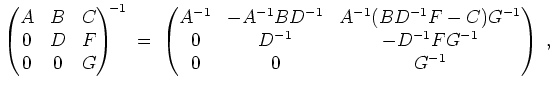
 verifiziert.
verifiziert.
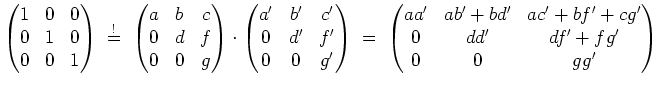
Die Gleichungen
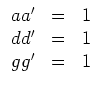
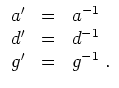
Dann liefern die Gleichungen
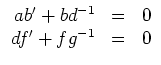
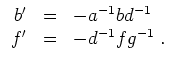
Schließlich folgt aus
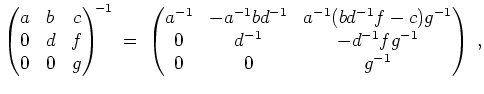
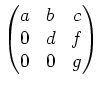 verifiziert.
verifiziert.
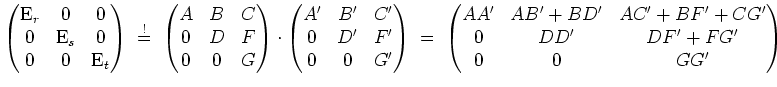
Die Gleichungen
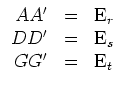
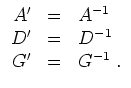
Dann liefern die Gleichungen
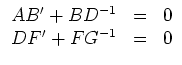
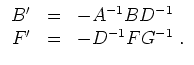
Schließlich folgt aus
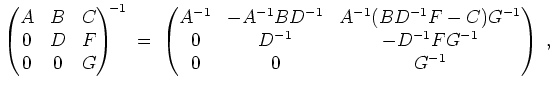
 verifiziert.
verifiziert.