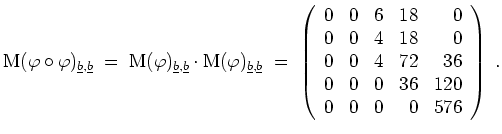![$ \mbox{$f(X),\, g(X)\,\in\,\mathbb{R}[X]$}$](img1.png){kind=small}
und
gilt
linear.
Durch Verkettung dieser Abbildung mit sich selbst folgt die Linearität der Abbildung
. Verkettet man schließlich die letztere Abbildung mit der Abbildung, welche ein Polynom mit
multipliziert, so erhält man die
Linearität der Abbildung
.
Verkettung von
mit
gibt die Linearität von
. Hierbei ist wegen
![$ \mbox{$g(X),\, h(X)\,\in\,\mathbb{R}[X]$}$](img11.png){kind=small}
und
die Abbildung
in der Tat linear.
Die Abbildung
ist nicht linear. So z.B. ist
, während
ist.
Die Abbildung
ist nicht linear. So z.B.
.
ist unter Vernachlässigung von Nullzeilen
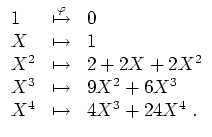
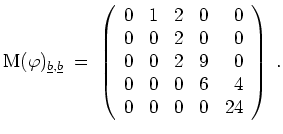
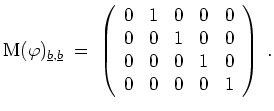
Also ist
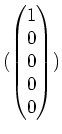eine Basis von
und
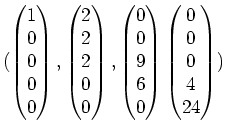eine Basis von
.
Folglich ist
(
) eine Basis von
und
eine Basis von
.
Da
ist, ist
nicht injektiv. Da
ist, ist
nicht surjektiv.
