Aufgabe.

Betrachte die Abbildungen

$ \mbox{$\displaystyle \begin{array}{rcl} \mathbb{R}[X] & \longrightarrow & \ma... ...\ f(X) & \mapsto & f(X)^2 \\ f(X) & \mapsto & f(f(X))\;. \\ \end{array}$}$

1.
Entscheide, welche Abbildungen dieser Liste linear sind. Begründe jeweils.
2.
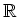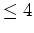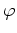Sei $ \mbox{$\mathbb{R}[X]_{\leq 4}$}$ der Vektorraum über $ \mbox{$\mathbb{R}$}$ der Polynome von Grad $ \mbox{$\leq 4$}$ . Sei $ \mbox{$\varphi$}$ die Summe der linearen Abbildungen dieser Liste, jeweils eingeschränkt zu einem Endomorphismus von $ \mbox{$\mathbb{R}[X]_{\leq 4}$}$ . Wähle eine Basis von $ \mbox{$\mathbb{R}[X]_{\leq 4}$}$ und gib die Darstellungsmatrix bezüglich dieser Basis an.
3.
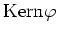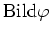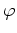Gib eine Basis von $ \mbox{$\text{Kern}\varphi$}$ und $ \mbox{$\text{Bild}\varphi$}$ an. Ist $ \mbox{$\varphi$}$ injektiv? Ist 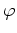$ \mbox{$\varphi$}$ surjektiv?
4.
Gib die Darstellungsmatrix von 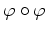$ \mbox{$\varphi\circ\varphi$}$ bezüglich der Basis in 2. an.