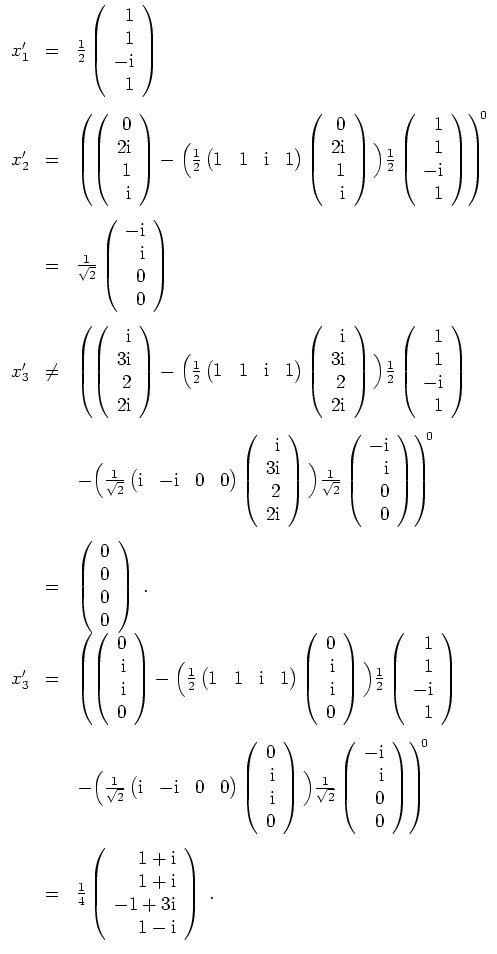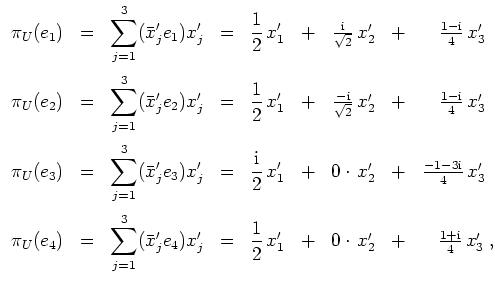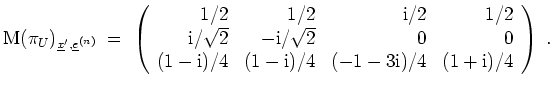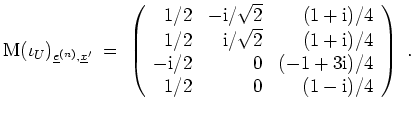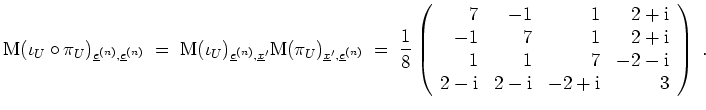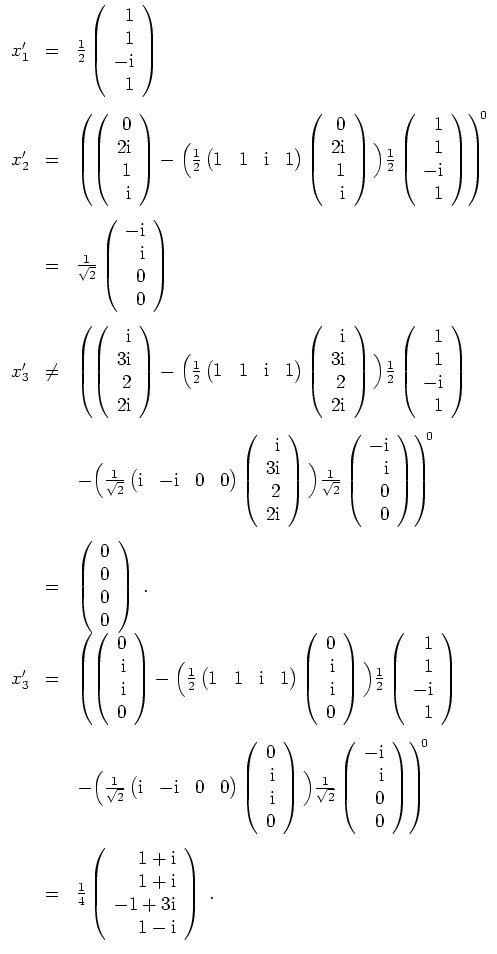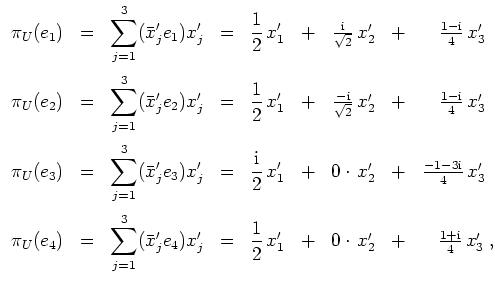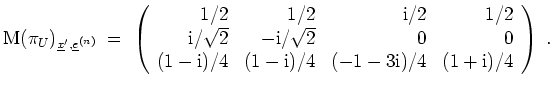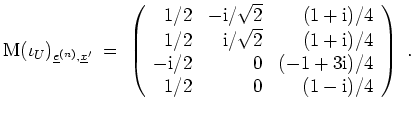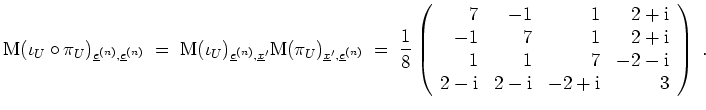Lösung.

1.
Mit Gram-Schmidt erhalten wir, unter Beachtung dessen, daß bei Entstehen eines Nullvektors direkt zum nächsten Schritt überzugehen ist,
$ \mbox{$\displaystyle \begin{array}{rcl} x'_1 & = & \frac{1}{2}\left(\begin{ar... ...m{i}\\ -1+3\mathrm{i}\\ 1-\mathrm{i}\end{array}\right)\; . \\ \end{array}$}$
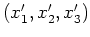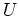Es ist $ \mbox{$(x'_1,x'_2,x'_3)$}$ eine Orthonormalbasis von $ \mbox{$U$}$ .
2.
Es wird
$ \mbox{$\displaystyle \begin{array}{rclcrcrcr} \pi_U(e_1) & = & \displaystyle ... ...\, x'_2 & + & \frac{1+\mathrm{i}}{4} \,x'_3\; ,\hspace*{-2mm}\\ \end{array}$}$
und somit
$ \mbox{$\displaystyle \text{M}(\pi_U)_{\underline{x}',\underline{e}^{(n)}} \;=... ...rm{i})/4 & (-1-3\mathrm{i})/4 & (1+\mathrm{i})/4 \\ \end{array}\right)\; . $}$
3.
Es ist
$ \mbox{$\displaystyle \text{M}(\iota_U)_{\underline{e}^{(n)},\underline{x}'} \... ...+3\mathrm{i})/4 \\ 1/2 & 0 & (1-\mathrm{i})/4 \\ \end{array}\right)\; . $}$
Damit wird
$ \mbox{$\displaystyle \text{M}(\iota_U\circ\pi_U)_{\underline{e}^{(n)},\underl... ... 2-\mathrm{i}& 2-\mathrm{i}& -2+\mathrm{i}& 3 \\ \end{array}\right)\; . $}$
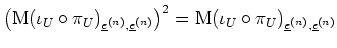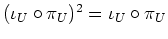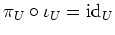Da $ \mbox{$\left(\text{M}(\iota_U\circ\pi_U)_{\underline{e}^{(n)},\underline{e}^{(... ...ht)^2 = \text{M}(\iota_U\circ\pi_U)_{\underline{e}^{(n)},\underline{e}^{(n)}}$}$ , ist in der Tat $ \mbox{$(\iota_U\circ\pi_U)^2 = \iota_U\circ\pi_U$}$ . Da $ \mbox{$\pi_U\circ\iota_U = {\mathrm{id}}_U$}$ , sollte dem auch so sein.