
Die Matrix
![]() ist (bis auf Weglassen von Nullzeilen) durch Multiplikation von A mit einer invertierbaren Matrix von links hervorgegangen. Somit
haben
ist (bis auf Weglassen von Nullzeilen) durch Multiplikation von A mit einer invertierbaren Matrix von links hervorgegangen. Somit
haben
![]() und
und
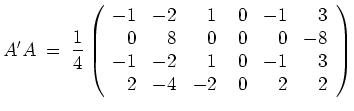
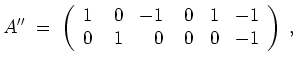
Es haben
![]() und
und
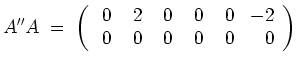
Es haben
![]() und
und
Sei
![]() ,
,
![]() . Sei
. Sei
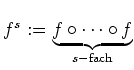 für
für
![]() . Insbesondere ist
. Insbesondere ist
![]() .
.
Aus
![]() folgt
folgt
Sei
![]() .
Sei
.
Sei
![]() die Spaltenstufenform von
die Spaltenstufenform von
![]() nach Streichung aller Nullspalten.
Sei
nach Streichung aller Nullspalten.
Sei
![]() die Spaltenstufenform von
die Spaltenstufenform von
![]() nach Streichung aller Nullspalten.
nach Streichung aller Nullspalten.
Sowohl die Spalten von
![]() als auch die Spalten von
als auch die Spalten von
![]() bilden eine Basis von
bilden eine Basis von
![]() (vgl. Beweis zu 3.).
(vgl. Beweis zu 3.).
Also gibt es eine invertierbare Matrix
![]() so, daß
so, daß
![]() . Da
. Da
![]() und
und
![]() sich in
Spaltenstufenform befinden und keine Nullspalten enthalten, folgt
sich in
Spaltenstufenform befinden und keine Nullspalten enthalten, folgt
![]() und
und
![]() .
.