- Es ist
Eine Abbildung dieser Form ist stets linear.
- Die Zeilenstufenform der aus
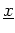 bzw.
bzw.
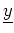 gebildeten Matrix ist jeweils die Einheitsmatrix.
Daher sind
gebildeten Matrix ist jeweils die Einheitsmatrix.
Daher sind
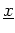 und
und
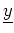 Basen des
Basen des
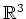 .
.
- Es wird
Also ist
Ferner wird
Also ist
Alternativ. Es wird
- Die Zeilenstufenform von
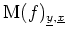 berechnet sich zu
Also ist
berechnet sich zu
Also ist
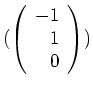 eine Basis von
eine Basis von
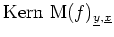 .
Es ist
und somit ist
.
Es ist
und somit ist
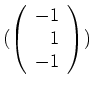 eine Basis von
eine Basis von
 .
.
- Die in 4. berechnete Zeilenstufenform von
 hat ausgewählte Spalten in Position
hat ausgewählte Spalten in Position
 und
und
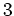 .
Also ist
.
Also ist
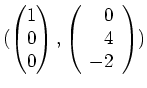 eine Basis von
eine Basis von
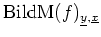 .
.
Es ist
und somit ist
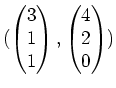 eine Basis von
eine Basis von
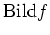 .
.
- Es gilt
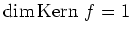 ,
,
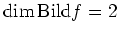 und in der Tat
und in der Tat
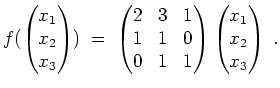
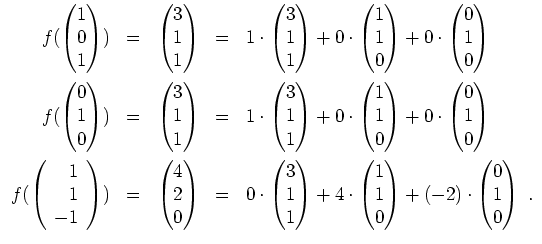
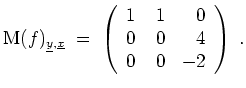
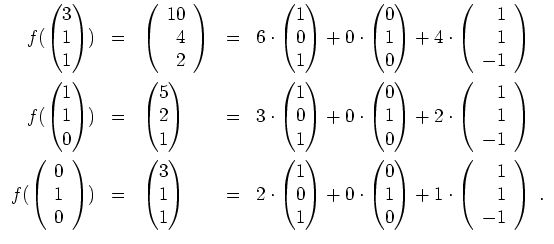
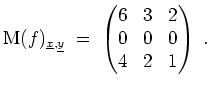
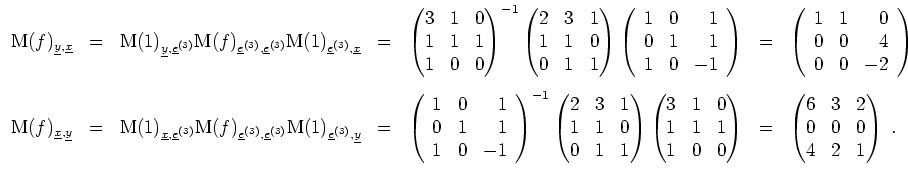
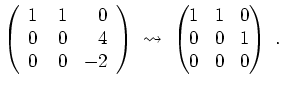
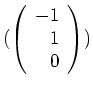 eine Basis von
eine Basis von
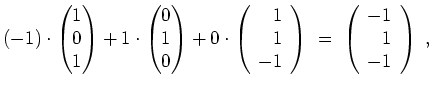
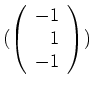 eine Basis von
eine Basis von
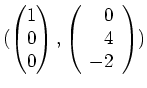 eine Basis von
eine Basis von
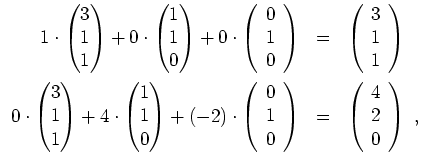
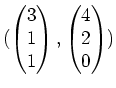 eine Basis von
eine Basis von
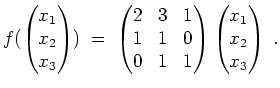
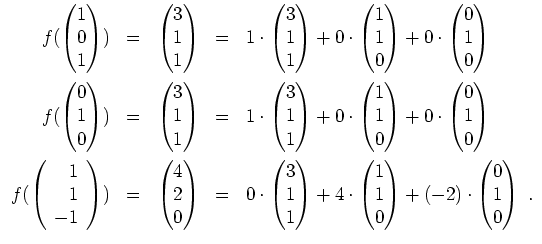
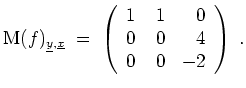
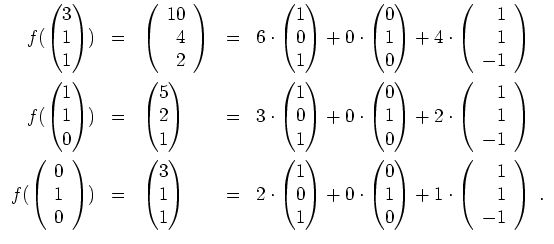
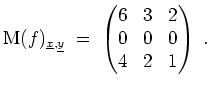
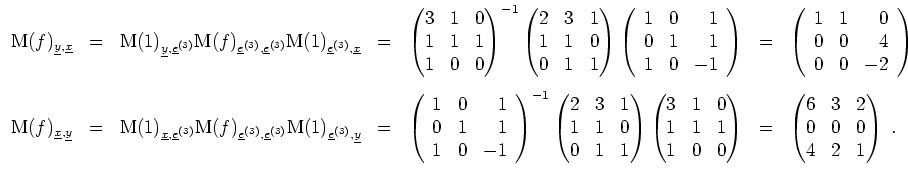
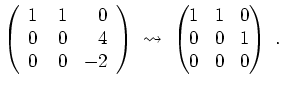
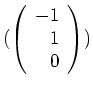 eine Basis von
eine Basis von
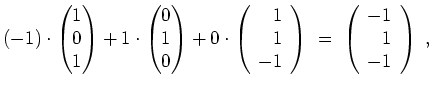
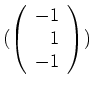 eine Basis von
eine Basis von
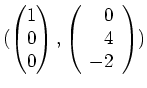 eine Basis von
eine Basis von
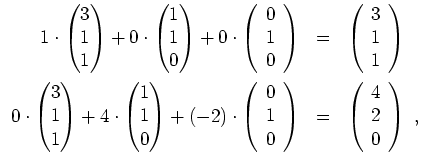
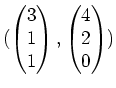 eine Basis von
eine Basis von