Beispiel.

Sei

$ \mbox{$\displaystyle A \;=\; \left( \begin{array}{rrrrrr} -4 & -11 & -2 & -3... ... & 2 & 0 & 1 & -1 \\ \end{array}\right) \;\in\; \mathbb{R}^{6\times 6}\; . $}$

1.
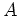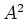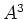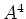Bestimme den Rang von $ \mbox{$A$}$ , $ \mbox{$A^2$}$ , $ \mbox{$A^3$}$ und $ \mbox{$A^4$}$ .
2.
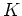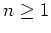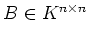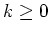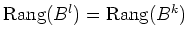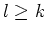Sei $ \mbox{$K$}$ ein Körper, sei $ \mbox{$n\geq 1$}$ , und sei $ \mbox{$B\in K^{n\times n}$}$ . Zeige, daß es ein $ \mbox{$k\geq 0$}$ gibt mit $ \mbox{$\text{Rang}(B^l) = \text{Rang}(B^k)$}$ für alle $ \mbox{$l\geq k$}$ .
3.
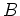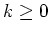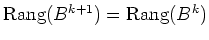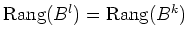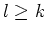Sei $ \mbox{$B$}$ wie in 2.. Sei $ \mbox{$k\geq 0$}$ . Zeige, daß aus $ \mbox{$\text{Rang}(B^{k+1}) = \text{Rang}(B^k)$}$ bereits folgt, daß $ \mbox{$\text{Rang}(B^l) = \text{Rang}(B^k)$}$ für alle $ \mbox{$l\geq k$}$ .
4.
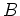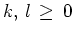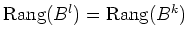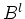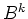Sei $ \mbox{$B$}$ wie in 2., und seien $ \mbox{$k,\, l\,\geq\, 0$}$ . Zeige, daß aus $ \mbox{$\text{Rang}(B^l) = \text{Rang}(B^k)$}$ folgt, daß die Zeilenstufenformen von $ \mbox{$B^l$}$ und $ \mbox{$B^k$}$ übereinstimmen.