Seien nun
![]() und
und
![]() . Dann gilt für alle
. Dann gilt für alle
![]()
Sei nun
![]() eine Basis von
eine Basis von
![]() . Wir ergänzen diese zu einer Basis
. Wir ergänzen diese zu einer Basis
![]() von
von
![]() .
Wendet man das Gram-Schmidtsche Orthonormalisierungsverfahren auf dieses Tupel an, so erhält man eine Orthonormalbasis
.
Wendet man das Gram-Schmidtsche Orthonormalisierungsverfahren auf dieses Tupel an, so erhält man eine Orthonormalbasis
![]() von
von
![]() derart, daß
derart, daß
![]() eine Orthonormalbasis von
eine Orthonormalbasis von
![]() ist.
Ferner gilt
ist.
Ferner gilt
![]() für
für
![]() .
.
Also gilt für jedes
![]() und jedes
und jedes
![]() , daß
, daß
 .
Wir wenden das Orthonormalisierungsverfahren von Gram-Schmidt auf diese Basis an. Dies liefert uns dann wie in der Lösung zu 2. die Orthonormalbasen
von
.
Wir wenden das Orthonormalisierungsverfahren von Gram-Schmidt auf diese Basis an. Dies liefert uns dann wie in der Lösung zu 2. die Orthonormalbasen
von
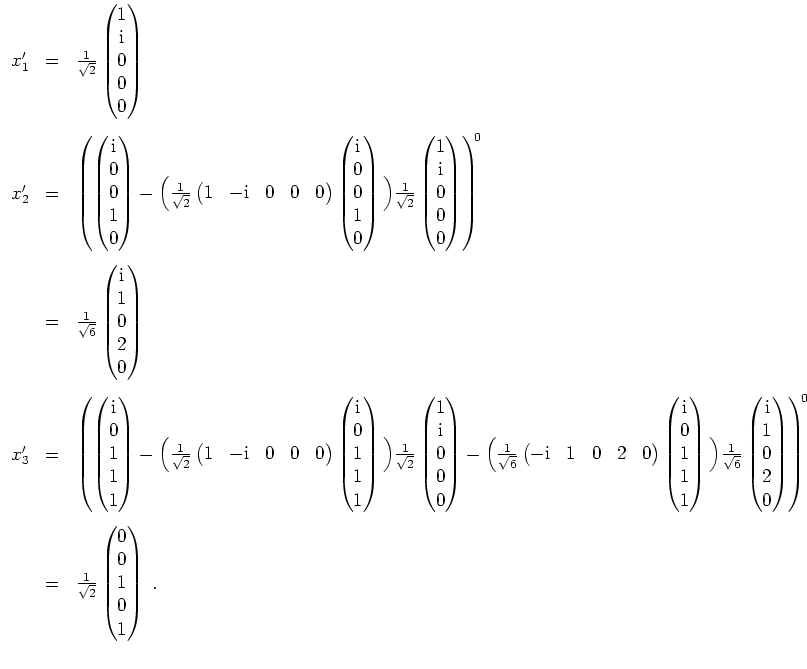
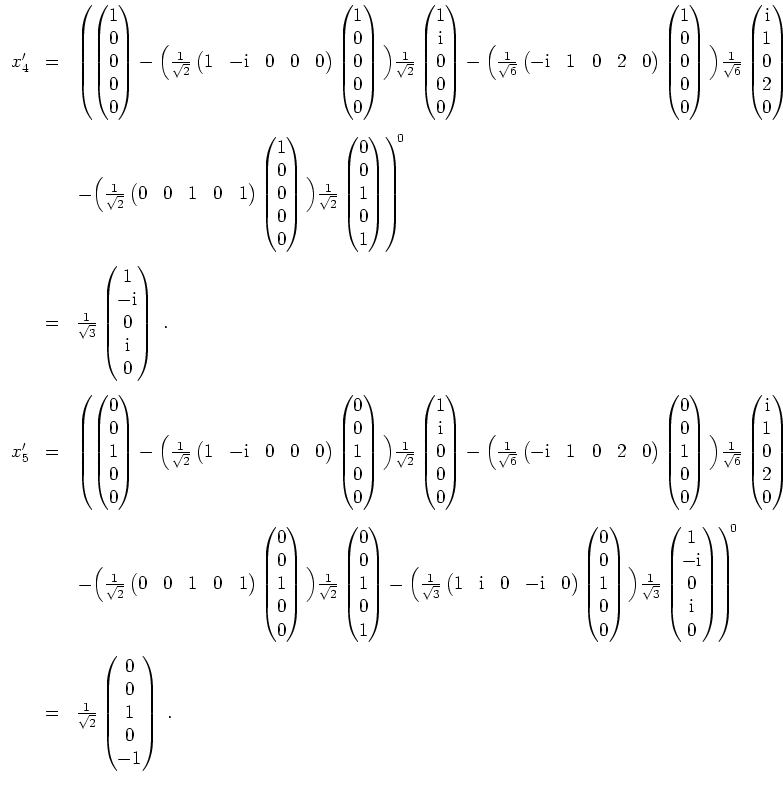
Damit ist
![]() eine Orthonormalbasis von
eine Orthonormalbasis von
![]() , und
, und
![]() eine Orthonormalbasis von
eine Orthonormalbasis von
![]() .
.