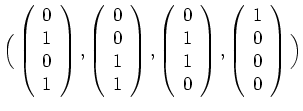 an, so erhalten wir
an, so erhalten wir
Wenden wir Gram-Schmidt auf das zu einer Basis ergänzte Tupel
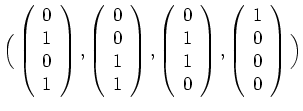 an, so erhalten wir
an, so erhalten wir
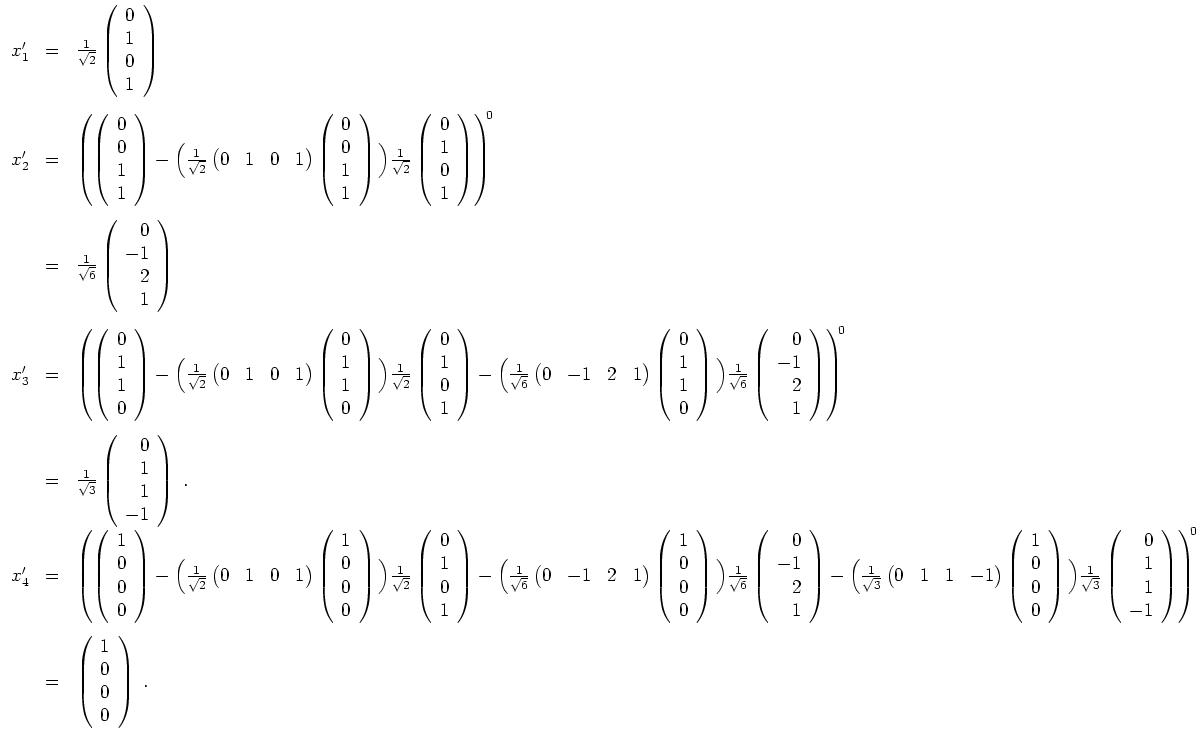
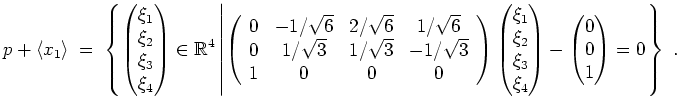
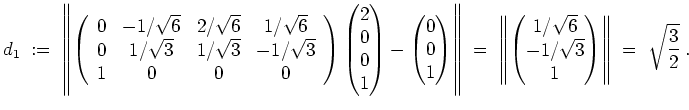
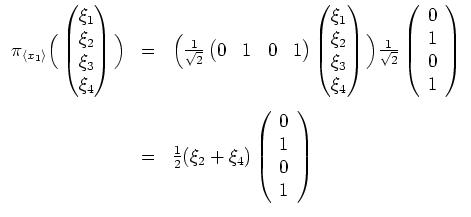
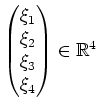 . Insbesondere wird
. Insbesondere wird
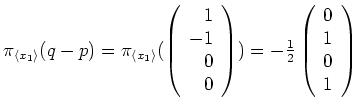 .
.
Der Cosinus des von
![]() und
und
![]() eingeschlossenen Winkels
eingeschlossenen Winkels
![]() ergibt sich damit zu
ergibt sich damit zu
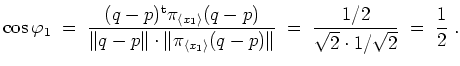
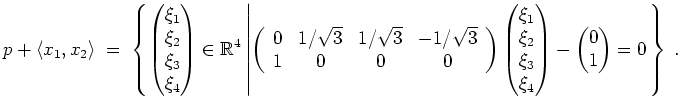
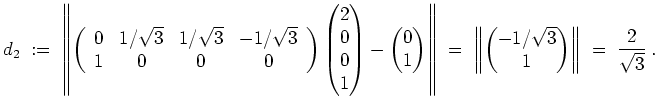
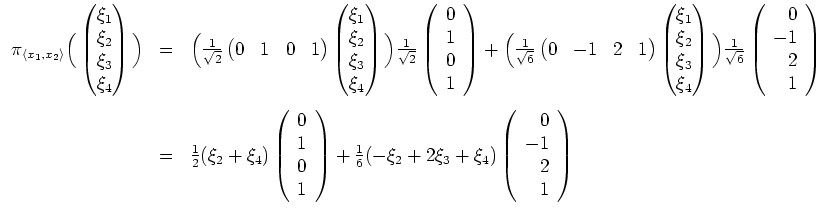
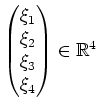 . Insbesondere wird
. Insbesondere wird
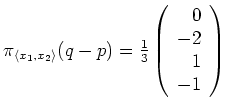 .
.
Der Cosinus des von
![]() und
und
![]() eingeschlossenen Winkels
eingeschlossenen Winkels
![]() ergibt sich damit zu
ergibt sich damit zu
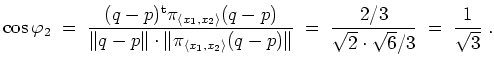
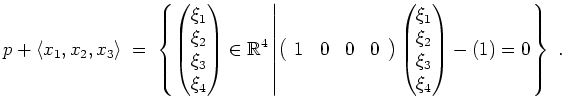
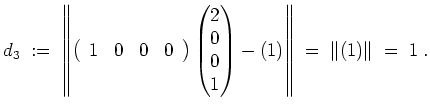
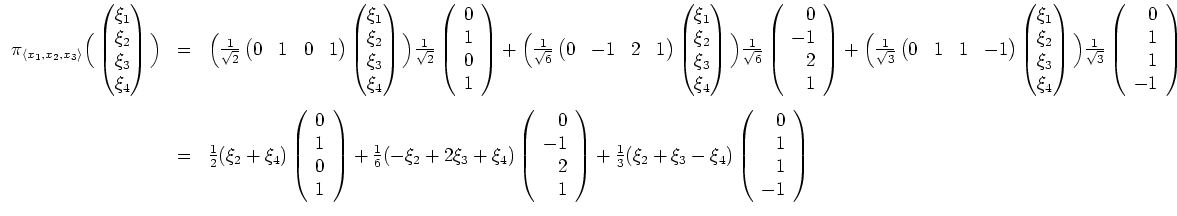
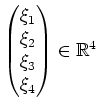 . Insbesondere wird
. Insbesondere wird
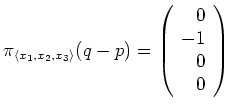 .
.
Der Cosinus des von
![]() und
und
![]() eingeschlossenen Winkels
eingeschlossenen Winkels
![]() ergibt sich damit zu
ergibt sich damit zu
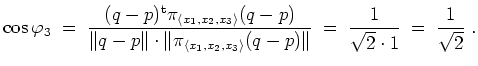
Wir beobachten, daß
![]() und
und
![]() , im Einklang mit der Anschauung.
, im Einklang mit der Anschauung.