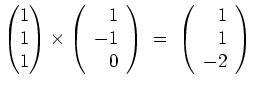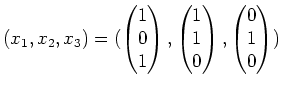Lösung.

1.
Gram-Schmidt, angewandt auf das ergänzte Tupel $ \mbox{$(x_1,x_2,x_3) = (\begin{pmatrix}1\\ 0\\ 1\end{pmatrix},\begin{pmatrix}1\\ 1\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1\\ 0\end{pmatrix})$}$ , gibt
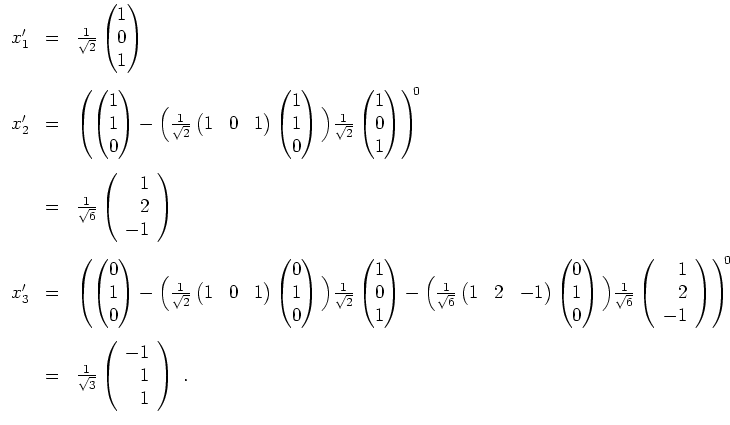
$ \mbox{$\displaystyle \begin{array}{rcl} x'_1 & = & \frac{1}{\sqrt{2}}\begin{p... ...{3}}\left(\begin{array}{r}-1\\ 1\\ 1\end{array}\right)\; . \\ \end{array}$}$
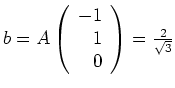
Damit erhalten wir $ \mbox{$A = \frac{1}{\sqrt{3}}\begin{pmatrix}-1&1&1\end{pmatrix}$}$ und $ \mbox{$b = A\left(\begin{array}{r}-1\\ 1\\ 0\end{array}\right) = \frac{2}{\sqrt{3}}$}$ $ \mbox{$(\in\mathbb{R}^1 =\mathbb{R})$}$ . Es wird
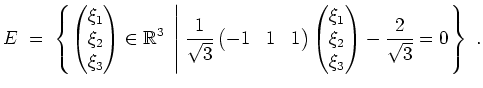
$ \mbox{$\displaystyle E \;=\; \left\{ \begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\e... ...1\\ \xi_2\\ \xi_3\end{pmatrix} - \frac{2}{\sqrt{3}} = 0\right.\right\}\; . $}$
Der Abstand von $ \mbox{$\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}$}$ zu $ \mbox{$E$}$ beträgt
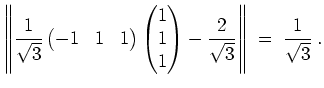
$ \mbox{$\displaystyle \left\Vert\frac{1}{\sqrt{3}}\begin{pmatrix}-1&1&1\end{pm... ... 1\end{pmatrix} - \frac{2}{\sqrt{3}}\right\Vert \;=\; \frac{1}{\sqrt{3}}\; . $}$

Alternativ erhält man den Vektor 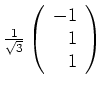$ \mbox{$\frac{1}{\sqrt{3}}\left(\begin{array}{r}-1\\ 1\\ 1\end{array}\right)$}$ , orthogonal zu den Erzeugern $ \mbox{$\begin{pmatrix}1\\ 0\\ 1\end{pmatrix}$}$ und $ \mbox{$\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}$}$ , auch als normierten Vektor von

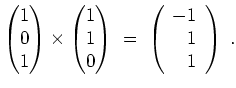
$ \mbox{$\displaystyle \begin{pmatrix}1\\ 0\\ 1\end{pmatrix} \times \begin{pm... ...\end{pmatrix} \;=\; \left(\begin{array}{r}-1\\ 1\\ 1\end{array}\right)\; . $}$

2.
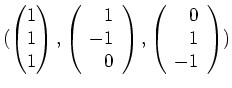Gram-Schmidt, angewandt auf das ergänzte Tupel $ \mbox{$(\begin{pmatrix}1\\ 1\\ 1\end{pmatrix},\left(\begin{array}{r}1\\ -1\\ 0\end{array}\right),\left(\begin{array}{r}0\\ 1\\ -1\end{array}\right))$}$ , gibt
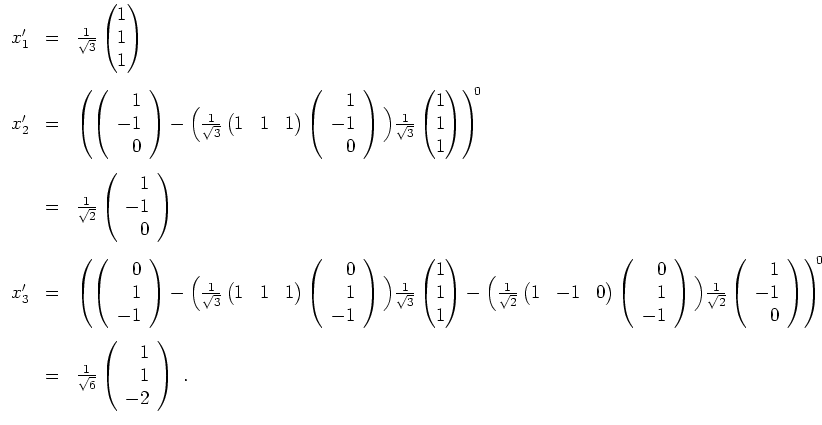
$ \mbox{$\displaystyle \begin{array}{rcl} x'_1 & = & \frac{1}{\sqrt{3}}\begin{p... ...{6}}\left(\begin{array}{r}1\\ 1\\ -2\end{array}\right)\; . \\ \end{array}$}$
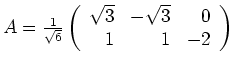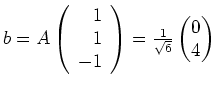Damit erhalten wir $ \mbox{$A = \frac{1}{\sqrt{6}}\left(\begin{array}{rrr}\sqrt{3}&-\sqrt{3}&0\\ 1&1&-2\end{array}\right)$}$ und $ \mbox{$b = A\left(\begin{array}{r}1\\ 1\\ -1\end{array}\right) = \frac{1}{\sqrt{6}}\begin{pmatrix}0 \\ 4\end{pmatrix}$}$ . Es wird
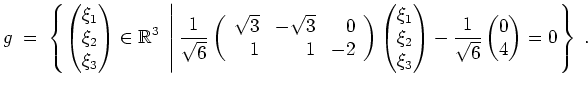
$ \mbox{$\displaystyle g \;=\; \left\{ \begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\e... ...\frac{1}{\sqrt{6}}\begin{pmatrix}0 \\ 4\end{pmatrix} = 0\right.\right\}\; . $}$
Der Abstand von $ \mbox{$\begin{pmatrix}1\\ 2\\ 1\end{pmatrix}$}$ zu $ \mbox{$g$}$ beträgt
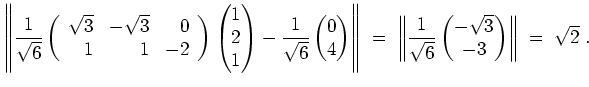
$ \mbox{$\displaystyle \left\Vert\frac{1}{\sqrt{6}}\left(\begin{array}{rrr}\sqr... ...}}\begin{pmatrix}-\sqrt{3}\\ -3\end{pmatrix}\right\Vert \;=\; \sqrt{2}\; . $}$

Alternativ, findet man einen Vektor wie 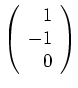$ \mbox{$\left(\begin{array}{r}1\\ -1\\ 0\end{array}\right)$}$ , der orthogonal zu $ \mbox{$\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}$}$ steht, so kann man den dritten Vektor einer Orthormalbasis als normierten Vektor von

$ \mbox{$\displaystyle \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\times \left(\beg... ...end{array}\right) \;=\; \left(\begin{array}{r}1\\ 1\\ -2\end{array}\right) $}$
finden.