- 1.
- Für
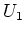 berechnen wir eine Zeilenstufenform
Die ausgewählten Spalten sind
berechnen wir eine Zeilenstufenform
Die ausgewählten Spalten sind
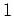 ,
,
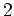 und
und
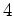 , und entsprechend können wir aus dem gegebenen erzeugenden Tupel Vektoren zu einer Basis
, und entsprechend können wir aus dem gegebenen erzeugenden Tupel Vektoren zu einer Basis
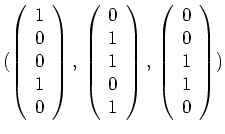 von
von
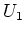 auswählen.
auswählen.
Für
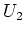 berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform
Die ausgewählten Spalten sind
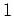 ,
,
 und
und
 , und entsprechend können wir aus dem gegebenen erzeugenden Tupel Vektoren zu einer Basis
, und entsprechend können wir aus dem gegebenen erzeugenden Tupel Vektoren zu einer Basis
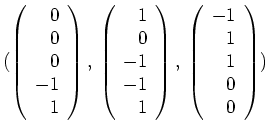 ausgewählt werden.
ausgewählt werden.
- 2.
-
Gemäß Zassenhaus-Algorithmus berechnen wir
Es war nicht direkt gefragt, nichtsdestoweniger können wir eine Basis
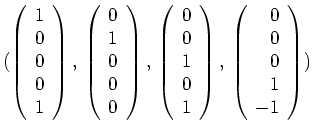 von
von
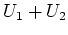 ablesen.
ablesen.
Darüberhinaus ist
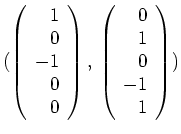 eine Basis von
eine Basis von
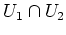 .
.
Insbesondere ist
was wir auch an der Zahl der Basisvektoren von
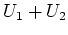 hätten erkennen können.
hätten erkennen können.

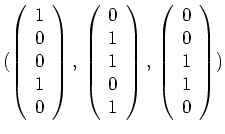 von
von
![]() berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform

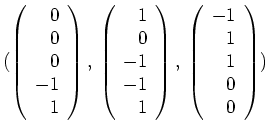 ausgewählt werden.
ausgewählt werden.

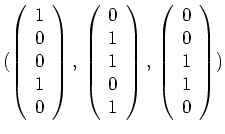 von
von
![]() berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform

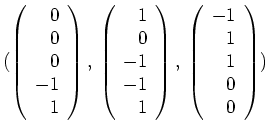 ausgewählt werden.
ausgewählt werden.

 von
von
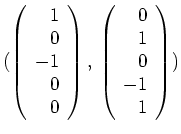 eine Basis von
eine Basis von
![]() .
.