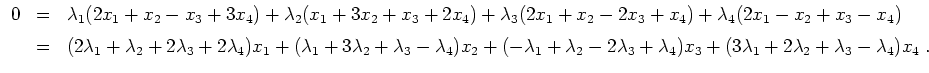
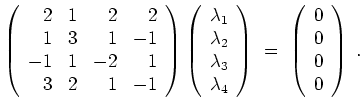

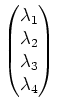
 haben.
haben.
Insbesondere ist das Tupel
![]() linear unabhängig, und wegen
linear unabhängig, und wegen
![]() also eine Basis von
also eine Basis von
![]() .
.
Es gilt
Ferner ist
![]() linear unabhängig, d.h.
linear unabhängig, d.h.
![]() . Nach der Dimensionsformel wird
. Nach der Dimensionsformel wird
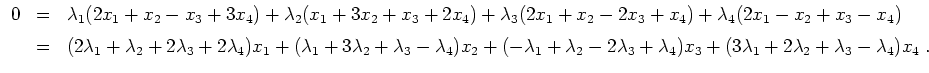
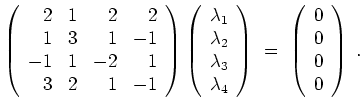

 haben.
haben.
Insbesondere ist das Tupel
![]() linear unabhängig, und wegen
linear unabhängig, und wegen
![]() also eine Basis von
also eine Basis von
![]() .
.
Es gilt
Ferner ist
![]() linear unabhängig, d.h.
linear unabhängig, d.h.
![]() . Nach der Dimensionsformel wird
. Nach der Dimensionsformel wird