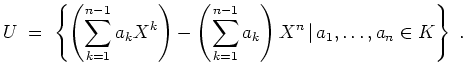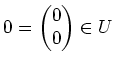 , weil
, weil
Seien nun
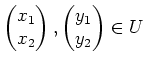 und
und
![]() .
Folglich gelten
.
Folglich gelten
![]() und
und
![]() .
Es wird
.
Es wird
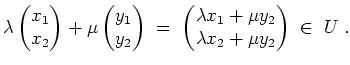
Ferner gilt (entsprechend dem Lösungsverfahren für lineare Gleichungssysteme)
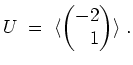
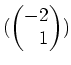 (von Länge
(von Länge
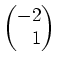 ungleich dem Nullvektor ist, ist dieses Tupel
auch linear unabhängig und bildet daher eine Basis von
ungleich dem Nullvektor ist, ist dieses Tupel
auch linear unabhängig und bildet daher eine Basis von
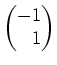 liegen beide in
liegen beide in
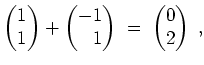
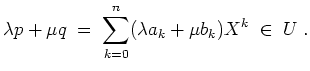
Nach der Definition der Polynome ist das Tupel der Monome
![]() linear unabhängig, denn eine
Linearkombination davon kann nur das Nullpolynom ergeben, wenn alle ihre Koeffizienten verschwinden.
linear unabhängig, denn eine
Linearkombination davon kann nur das Nullpolynom ergeben, wenn alle ihre Koeffizienten verschwinden.
Da es auch erzeugend ist, bildet
![]() eine Basis von
eine Basis von
![]() , und es ist
, und es ist
![]() .
.
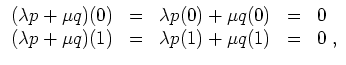
Wegen
![]() und
und
![]() für
für
![]() folgt
folgt