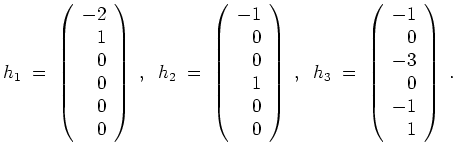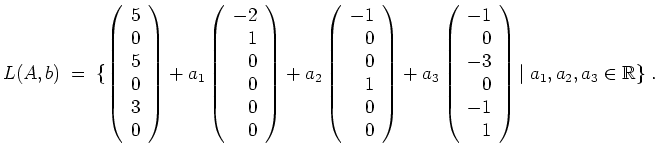Lösung.

Wir schreiben das Gleichungssystem in Matrixform $ \mbox{$Ax=b$}$ , und wenden den Gaußschen Algorithmus auf die erweiterte Matrix $ \mbox{$(A\vert b)$}$ an. Es wird

$ \mbox{$\displaystyle \begin{array}{rl} &\left(\begin{array}{rrrrrr\vert l} ... ...& 0& 0& 0& 1& 1& 3\\ 0& 0& 0& 0& 0& 0& 0 \end{array}\right)\;. \end{array}$}$
Die ausgewählten Spalten sind $ \mbox{$k_1 = 1$}$ , $ \mbox{$k_2 = 3$}$ und $ \mbox{$k_3 = 5$}$ . Die nicht ausgewählten Spalten sind $ \mbox{$k'_1 = 2$}$ , $ \mbox{$k'_2 = 4$}$ und $ \mbox{$k'_3 = 6$}$ .

Eine partikuläre Lösung ist (durch positives Einfüllen)

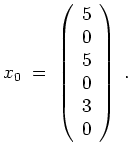
$ \mbox{$\displaystyle x_0 \; =\; \left(\begin{array}{r}5\\ 0\\ 5\\ 0\\ 3\\ 0\end{array}\right)\;. $}$

Lösungen des zugehörigen homogenen Gleichungssystems sind also (durch negatives Einfüllen)

$ \mbox{$\displaystyle h_1 \; =\; \left(\begin{array}{r} -2\\ 1\\ 0\\ 0\\ 0... ...; \left(\begin{array}{r} -1\\ 0\\ -3\\ 0\\ -1\\ 1\end{array}\right)\; . $}$
Die Lösungsmenge des Gleichungssystems ist also
$ \mbox{$\displaystyle L(A,b) \;=\; \{ \left(\begin{array}{r} 5\\ 0\\ 5\\ 0... ... -3\\ 0\\ -1\\ 1\end{array}\right) \vert\; a_1,a_2,a_3\in\mathbb{R}\}\;. $}$