Lösung.

Es handelt sich um eine autonome Gleichung. Wir setzen $ \mbox{$\dot{x}=v(x)$}$, d.h. $ \mbox{$v$}$ gibt die Geschwindigkeit in Abhängigkeit des Ortes an.

Dies führt zur Gleichung

$ \mbox{$\displaystyle 0 \; =\; mvv' + Dx - Rv^2\; , $}$
also zu
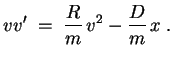
$ \mbox{$\displaystyle vv' \;=\; \frac{R}{m}\, v^2 - \frac{D}{m}\,x\;. $}$
Diese Gleichung für $ \mbox{$v$}$ ist eine Bernoullische Gleichung mit Exponent $ \mbox{$\alpha=-1$}$. Die Substitution $ \mbox{$\eta=v^2$}$ führt zu
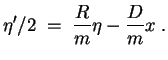
$ \mbox{$\displaystyle \eta'/2 \;=\; \frac{R}{m}\eta - \frac{D}{m} x\;. $}$
Dies ist eine inhomogene Gleichung.

Die allgemeine Lösung der zugehörigen homogenen Gleichung $ \mbox{$\eta'=\frac{2R}{m}\eta$}$ ist $ \mbox{$\eta = c\exp(2Rx/m)$}$ mit einer Konstanten $ \mbox{$c\in\mathbb{R}$}$. Eine partikuläre Lösung für die inhomogene Gleichung findet man durch Variation der Konstanten, also durch den Ansatz $ \mbox{$\eta=c(x)\exp(2Rx/m)$}$. Dies führt auf

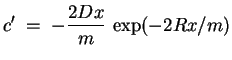
$ \mbox{$\displaystyle c' \;=\; -\frac{2Dx}{m}\,\exp(-2Rx/m) $}$
und also auf
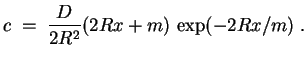
$ \mbox{$\displaystyle c \;=\; \frac{D}{2R^2}(2Rx+m)\,\exp(-2Rx/m)\; . $}$
Die allgemeine Lösung für $ \mbox{$\eta$}$ ist folglich
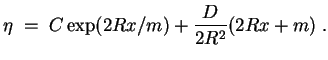
$ \mbox{$\displaystyle \eta \;=\; C\exp(2Rx/m) + \frac{D}{2R^2}(2Rx+m) \; . $}$
mit einer Konstanten $ \mbox{$C\in\mathbb{R}$}$. Somit ist aus physikalischen Gründen
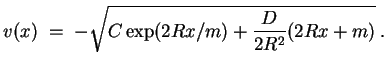
$ \mbox{$\displaystyle v(x) \; = \; -\sqrt{C\exp(2Rx/m) + \frac{D}{2R^2}(2Rx+m)}\; . $}$
negativ, und also
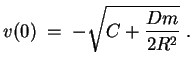
$ \mbox{$\displaystyle v(0) \; = \; -\sqrt{C + \frac{Dm}{2R^2}\right)}\; . $}$
Es bleibt uns, die Konstante $ \mbox{$C$}$ zu bestimmen. Es sollte
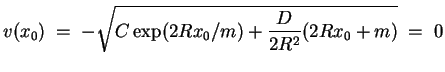
$ \mbox{$\displaystyle v(x_0) \; =\; -\sqrt{C\exp(2Rx_0/m) + \frac{D}{2R^2}(2Rx_0+m)} \; =\; 0 $}$
sein, d.h.
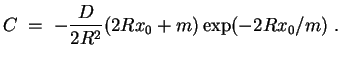
$ \mbox{$\displaystyle C\; =\; -\frac{D}{2R^2} (2Rx_0+m)\exp(-2Rx_0/m)\; . $}$

Skizze des Verlaufs von $ \mbox{$x(t)$}$ im Falle $ \mbox{$m=1$}$, $ \mbox{$D=1$}$ und $ \mbox{$R=1$}$ für einige Anfangswerte.

\includegraphics[width=10cm]{s1_osz.eps}