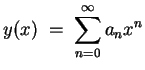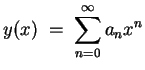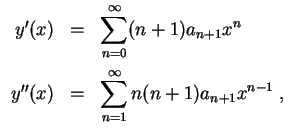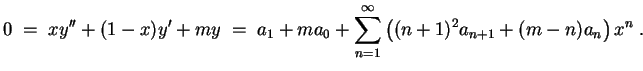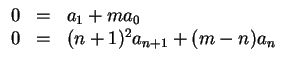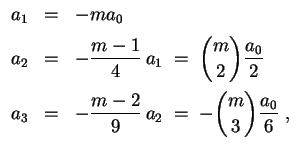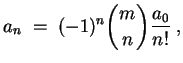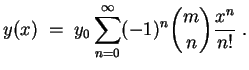Mit dem Ansatz
ergibt sich
und daher
Dies liefert durch Koeffizientenvergleich
für alle
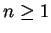 . Daraus kann man rekursiv berechnen
usf. Allgemein ergibt sich als Lösung dieser Rekursion
und die gesuchte Potenzreihe lautet wegen
. Daraus kann man rekursiv berechnen
usf. Allgemein ergibt sich als Lösung dieser Rekursion
und die gesuchte Potenzreihe lautet wegen
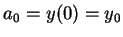 Diese Potenzreihe konvergiert für alle
Diese Potenzreihe konvergiert für alle
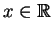 .
.