Lösung.

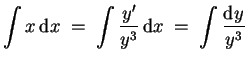
Durch Trennung der Variablen ergibt sich

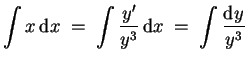
$ \mbox{$\displaystyle \displaystyle\int x\,{\mbox{d}}x \;=\; \displaystyle\int \frac{y'}{y^3}\,{\mbox{d}}x \;=\; \displaystyle\int \frac{{\mbox{d}}y}{y^3} $}$
und folglich
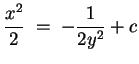
$ \mbox{$\displaystyle \frac{x^2}{2} \;=\; -\frac{1}{2y^2}+c $}$
mit einer Konstanten $ \mbox{$c\in\mathbb{R}$}$. Auflösen nach $ \mbox{$y$}$ liefert
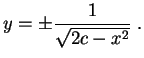
$ \mbox{$\displaystyle y=\pm\frac{1}{\sqrt{2c-x^2}} \;. $}$
Hier muß $ \mbox{$c>0$}$ gefordert werden, und dann ist die Lösung $ \mbox{$y$}$ auf dem Intervall $ \mbox{$(-\sqrt{2c},+\sqrt{2c})$}$ erklärt.

Weiter erhält man aufgrund der Nullstelle $ \mbox{$0$}$ von $ \mbox{$g(y)=y^3$}$ die konstante Lösung $ \mbox{$y(x)=0$}$; diese entspricht sozusagen $ \mbox{$c=+\infty$}$.

Die Differentialgleichung $ \mbox{$y'=yx^3$}$ gibt in jedem Punkt die Steigung einer Lösung vor. Man erhält auf diese Weise ein Richtungsfeld.

\includegraphics[width=10cm]{e1_dfield.eps}