Lösung.

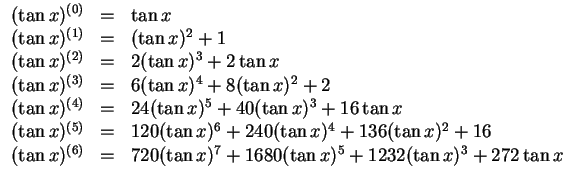
Wir bilden zunächst einmal die iterierten Ableitungen.

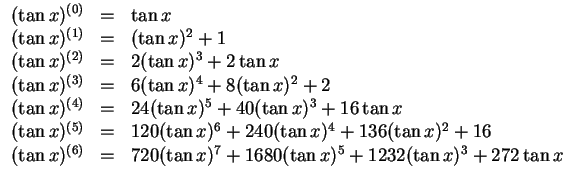
$ \mbox{$\displaystyle \begin{array}{rcl} (\tan x)^{(0)} & = & \tan x \\ (\ta... ... 720(\tan x)^7 + 1680(\tan x)^5 + 1232(\tan x)^3 + 272\tan x \\ \end{array}$}$
Mit $ \mbox{$\tan 0 = 0$}$ erhalten wir die Taylorentwicklung für $ \mbox{$n = 5$}$
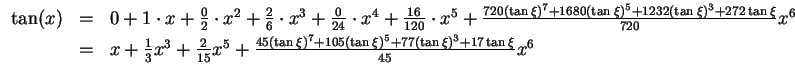
$ \mbox{$\displaystyle \begin{array}{rcl} \tan(x) & = & 0 + 1\cdot x + \frac{0... ...\xi)^7 + 105(\tan\xi)^5 + 77(\tan\xi)^3 + 17\tan\xi}{45} x^6 \\ \end{array}$}$
für ein $ \mbox{$\xi$}$ zwischen $ \mbox{$0$}$ und $ \mbox{$x$}$.

Wir bemerken noch, daß nur die Koeffizienten mit ungeradem Index in der Taylorentwicklung um $ \mbox{$0$}$ nicht verschwinden, da es sich bei $ \mbox{$\tan x$}$ um eine ungerade Funktion handelt.

Im Restglied geht $ \mbox{$45(\tan\xi)^7 + 105(\tan\xi)^5 + 77(\tan\xi)^3 + 17\tan\xi$}$ gegen $ \mbox{$+\infty$}$ für $ \mbox{$\xi\to\pi/2$}$. Da wir für $ \mbox{$x\to\pi/2$}$ auch nicht ausschließen können, daß sich $ \mbox{$\xi$}$ nahe bei $ \mbox{$\pi/2$}$ befindet, erhalten wir über das Restglied keine Schranken für die Approximation von $ \mbox{$\tan x$}$ durch $ \mbox{$x + \frac{1}{3} x^3 + \frac{2}{15} x^5$}$. Da $ \mbox{$\tan x$}$ im Gegensatz zu diesem Polynom auf $ \mbox{$(-\pi/2,+\pi/2)$}$ unbeschränkt ist, kann eine solche Schranke auch nicht existieren.