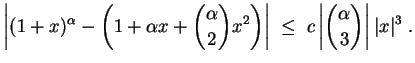- Die Taylorentwicklung von
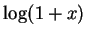 um
um
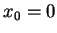 mit
mit
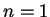 liefert ein
liefert ein
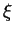 zwischen
zwischen
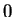 und
und
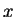 so, daß
Wegen
so, daß
Wegen
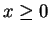 ist
ist
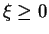 , also gilt
, also gilt
- Hier ist
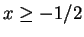 , also auch
, also auch
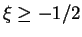 und
und
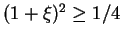 . Daraus folgt mit dem Ansatz aus (1)
. Daraus folgt mit dem Ansatz aus (1)
- Die Taylorentwicklung von
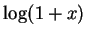 um
um
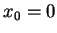 mit
mit
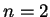 liefert ein
liefert ein
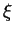 zwischen
zwischen
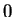 und
und
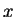 so, daß
Wegen
so, daß
Wegen
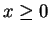 ist
ist
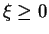 , also gilt
, also gilt
- Die Taylorentwicklung von
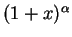 um
um
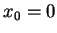 mit
mit
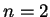 liefert ein
liefert ein
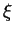 zwischen
zwischen
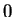 und
und
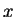 so, daß
so, daß
Im Falle
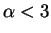 ist
ist
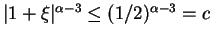 .
.
Im Falle
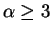 ist
ist
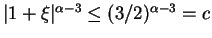 .
.
Also folgt
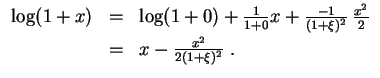
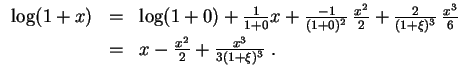
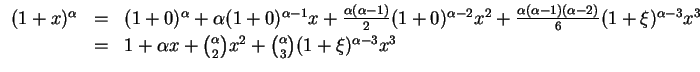
![]() ist
ist
![]() .
.
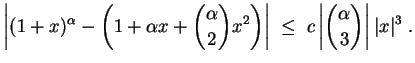
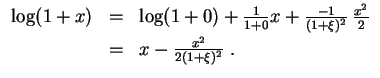
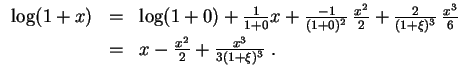
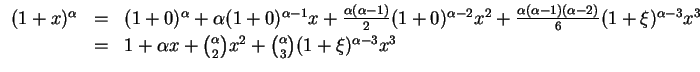
![]() ist
ist
![]() .
.